Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
0. Functions
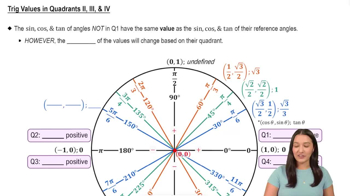
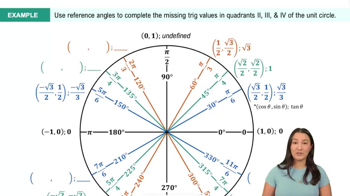
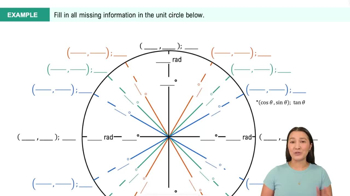
Introduction to Trigonometric Functions
Problem 45
Textbook Question
Solve the following equations.
{Use of Tech} sin2θ=51,0<θ<2π
 Verified step by step guidance
Verified step by step guidance1
First, recognize that the equation given is \( \sin 2\theta = \frac{1}{5} \). This is a trigonometric equation involving the sine function.
Next, use the inverse sine function to solve for \( 2\theta \). This gives \( 2\theta = \arcsin\left(\frac{1}{5}\right) \).
Since the sine function is periodic with a period of \( 2\pi \), consider the general solution for \( 2\theta \), which is \( 2\theta = \arcsin\left(\frac{1}{5}\right) + 2k\pi \) or \( 2\theta = \pi - \arcsin\left(\frac{1}{5}\right) + 2k\pi \), where \( k \) is an integer.
Now, solve for \( \theta \) by dividing the entire equation by 2, giving \( \theta = \frac{1}{2}\arcsin\left(\frac{1}{5}\right) + k\pi \) or \( \theta = \frac{1}{2}(\pi - \arcsin\left(\frac{1}{5}\right)) + k\pi \).
Finally, apply the constraint \( 0 < \theta < \frac{\pi}{2} \) to find the specific values of \( \theta \) that satisfy the original equation within the given interval. Check each possible solution to ensure it falls within this range.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?

 5:4m
5:4mWatch next
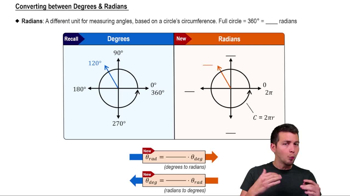
Master Converting between Degrees & Radians with a bite sized video explanation from Patrick Ford
Start learning