Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
2. Intro to Derivatives
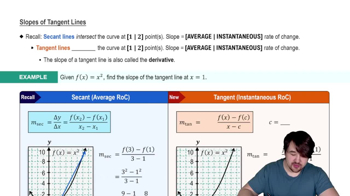
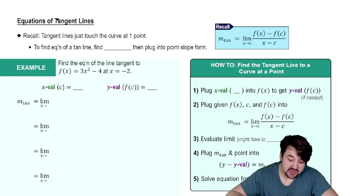
Tangent Lines and Derivatives
Problem 39a
Textbook Question
Find the derivative function f' for the following functions f.
f(x) = 2/3x+1; a= -1
 Verified step by step guidance
Verified step by step guidance1
Step 1: Identify the function f(x) = \frac{2}{3}x + 1. This is a linear function of the form f(x) = ax + b, where a = \frac{2}{3} and b = 1.
Step 2: Recall that the derivative of a linear function f(x) = ax + b is simply the coefficient of x, which is a. In this case, the derivative f'(x) will be \frac{2}{3}.
Step 3: Since the derivative of a constant is zero, the +1 in the function does not affect the derivative. Therefore, f'(x) = \frac{2}{3}.
Step 4: Evaluate the derivative at the given point a = -1. Since the derivative is constant, f'(-1) = \frac{2}{3}.
Step 5: Conclude that the derivative function f'(x) is constant and equal to \frac{2}{3} for all x, including at x = -1.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Derivative
The derivative of a function measures how the function's output value changes as its input value changes. It is defined as the limit of the average rate of change of the function over an interval as the interval approaches zero. The derivative is often denoted as f'(x) and represents the slope of the tangent line to the function's graph at any given point.
Recommended video:

Derivatives
Power Rule
The Power Rule is a fundamental technique for finding derivatives of polynomial functions. It states that if f(x) = x^n, where n is a real number, then the derivative f'(x) = n*x^(n-1). This rule simplifies the process of differentiation, especially for functions that can be expressed in polynomial form.
Recommended video:
Guided course

Power Rules
Constant Rule
The Constant Rule states that the derivative of a constant is zero. This means that if a function f(x) is a constant value, its rate of change is zero, indicating that the function does not change regardless of the input. This rule is essential when differentiating functions that include constant terms.
Recommended video:

The Power Rule

 5:13m
5:13mWatch next
Master Slopes of Tangent Lines with a bite sized video explanation from Nick
Start learningRelated Videos
Related Practice