Intro to Extrema: Videos & Practice Problems

Extrema on a graph include global extrema, which are the highest and lowest points of the entire function, and local extrema, which are the highest and lowest points within a specific region. A global maximum occurs when $f\left(c\right)>=f\left(x\right)$ for all $x$, while a local maximum is defined similarly but only for nearby points. Understanding these concepts is crucial for analyzing functions effectively.

Finding Extrema Graphically

Understanding extrema is crucial in analyzing the behavior of functions. Extrema refer to the maximum and minimum values of a function, and they can be categorized into two types: global (or absolute) extrema and local (or relative) extrema. Global extrema are the highest and lowest points of the entire function, while local extrema are the highest and lowest points within a specific region of the function.

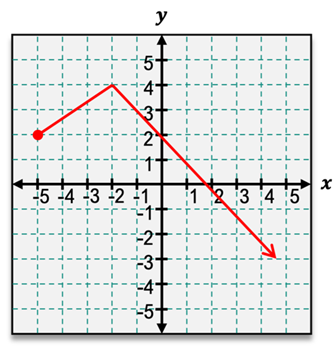
To identify a global maximum, we consider a point \( c \) in the function. If the function value at this point, \( f(c) \), is greater than or equal to \( f(x) \) for all other \( x \) values in the function, then \( c \) represents a global maximum. Conversely, a global minimum occurs at point \( c \) if \( f(c) \) is less than or equal to \( f(x) \) for all \( x \). For example, if the highest point of a function is at \( (-3, 5) \), we can express this as the global maximum value of 5 at \( x = -3 \).

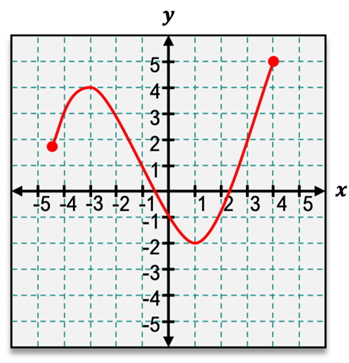
Local extrema, on the other hand, focus on a smaller section of the graph. A local maximum occurs at point \( c \) if \( f(c) \) is greater than or equal to \( f(x) \) for all nearby \( x \) values. Similarly, a local minimum occurs if \( f(c) \) is less than or equal to \( f(x) \) for nearby \( x \) values. This means that local extrema can be visualized as peaks and valleys within a specific region of the graph.

It is also important to note that a point can be both a global and a local extremum. For instance, if the global maximum is also the highest point in its immediate vicinity, it qualifies as both. However, endpoints of a function can be global extrema but typically do not qualify as local extrema due to their nature as boundaries. This distinction can vary based on conventions used in different courses, so it is advisable to confirm the specific definitions with your instructor.

In summary, recognizing the difference between global and local extrema is essential for understanding the overall behavior of functions. By analyzing the entire function for global extrema and focusing on specific regions for local extrema, one can gain deeper insights into the function's characteristics.

Finding Extrema Graphically Example 1

In analyzing the extreme values of a function defined over various domains, it is essential to understand the concepts of global and local extrema. The function in question is examined across three different domains, each yielding distinct results regarding its extreme values.

For the first graph, where the function is defined over all real numbers (from negative infinity to positive infinity), the absolute lowest point occurs at \(x = 0\). This point represents both a global minimum and a local minimum, as it is the lowest value compared to all nearby points. However, since the function continues to rise indefinitely on both sides, there are no maximum values present. Thus, this function has a global and local minimum at \(f(0) = 0\) and no maximum values.

In the second graph, the function is restricted to the domain from \(0\) to \(3\), including both endpoints. Here, the global minimum is again at \(x = 0\) with a value of \(f(0) = 0\). However, this point cannot be classified as a local minimum due to the convention that endpoints are not considered local extrema. The global maximum occurs at \(x = 3\), where the function reaches a value of \(f(3) = 9\). Therefore, this function has a global minimum of \(0\) at \(x = 0\) and a global maximum of \(9\) at \(x = 3\), with no local extrema.

In the final graph, the domain is again from \(0\) to \(3\), but this time the endpoints are excluded. Although the function approaches \(0\) as \(x\) approaches \(0\) from the right, it never actually reaches this value, meaning there is no global minimum. Similarly, as \(x\) approaches \(3\), the function can get arbitrarily close to its maximum value but does not include it, resulting in no global maximum either. Consequently, this function has no extreme values due to the exclusion of the endpoints.

These examples illustrate how the definition of the domain significantly impacts the identification of extreme values. Understanding the distinction between global and local extrema, especially in relation to endpoints, is crucial for accurately determining the behavior of functions across different intervals.

Finding Extrema Graphically Example 2

In analyzing the function f(x) for local and global maxima and minima, it is essential to identify the peaks and valleys on the graph. The highest point of the function occurs at x = -2, which is classified as the global maximum since it represents the highest value across the entire function. Additionally, this point is also a local maximum because it is the highest point in its immediate vicinity.

Conversely, the lowest point of the function is found at x = 1, where f(1) = -5. This point serves as the global minimum, as it is the lowest value of the function overall, and it is also a local minimum since it is the lowest point among nearby values.

Further examination reveals additional local extrema. At x = -4, a local minimum is identified, as it is the lowest point in that region of the graph. On the other hand, at x = 3, a local maximum is present, being the highest point among its neighboring values. Lastly, another local minimum occurs at x = 5, where it is lower than the surrounding points.

It is important to note that endpoints of the function are not considered local extrema in this context. Therefore, while we have identified the global maximum and minimum, as well as several local maxima and minima, the endpoints do not contribute to extreme values.

Determine where the local and absolute maxima and minima occur on the given graph of $f\left(x\right)$.

• A. Absolute max of 4 at $x=-2$, Absolute min of $-3$ at $x=5$
• B. Absolute max of 4 at $x=-2$, Local max of 4 at $x=-2$, No absolute or local mins
• C. Absolute max of 4 at $x=-2$, Absolute min of 2 at $x=-5$
• D. Absolute max of 4 at $x=-2$, Local max of 4 at $x=-2$, Local min of 2 at $x=-5$

Answer: (B)

Determine where the local and absolute maxima and minima occur on the given graph of $f\left(x\right)$.

• A. Absolute max of 5 at $x=4$, Local max of 4 at $x=-3$, Absolute min of $-2$ at $x=1$, Local min of $-2$ at $x=1$ & 1.5 at $x=-4.5$
• B. Absolute max of 5 at $x=4$, Absolute min of $-2$ at $x=1$, No local extrema
• C. Absolute max of 4 at $x=-3$, Local max of 4 at $x=-3$, Absolute min of $-2$ at $x=1$, Local min of $-2$ at $x=1$
• D. Absolute max of 5 at $x=4$, Local max of 4 at $x=-3$, Absolute min of $-2$ at $x=1$, Local min of $-2$ at $x=1$$x=1$

Answer: (D)

Finding Extrema Graphically Example 3

To sketch a graph of a function that is continuous over the interval from -3 to 2, we need to incorporate specific properties regarding its maximum and minimum values. The function must have an absolute maximum at \( x = 2 \), an absolute minimum at \( x = 0 \), and a local maximum at \( x = -2 \). The endpoints at \( x = -3 \) and \( x = 2 \) will be included in the graph, represented by solid dots.

Starting with the absolute maximum at \( x = 2 \), this point must be the highest value of the function within the specified interval. We can place this point at a higher value on the y-axis, ensuring it is the peak of the graph. Next, the absolute minimum at \( x = 0 \) should be the lowest point of the function, resembling a valley or downward peak. This point will be positioned lower on the graph.

For the local maximum at \( x = -2 \), we need to create a peak that is higher than the values immediately surrounding it but lower than the absolute maximum at \( x = 2 \). This ensures that it is a local maximum, as it does not exceed the overall highest point of the function.

Finally, we must include the endpoint at \( x = -3 \). This point will not be an extreme value but will serve as the starting point of our graph. The function must be continuous, meaning there should be no breaks or holes in the graph as we connect these points.

In summary, the graph will start at the endpoint \( x = -3 \), rise to the local maximum at \( x = -2 \), drop down to the absolute minimum at \( x = 0 \), and then rise again to reach the absolute maximum at \( x = 2 \). This structure ensures that all specified properties are satisfied, resulting in a smooth, continuous function that adheres to the given conditions.

Here’s what students ask on this topic:

What is the difference between global extrema and local extrema?

Global extrema refer to the highest and lowest points of an entire function, known as the global maximum and global minimum. These points are the absolute highest and lowest values that the function reaches. Local extrema, on the other hand, are the highest and lowest points within a specific region of the function. These are known as local maximum and local minimum. While global extrema consider the entire function, local extrema only consider nearby points within a small region.

How do you identify a global maximum on a graph?

To identify a global maximum on a graph, you need to find the highest point of the entire function. This point occurs where the function value, f(c), is greater than or equal to all other function values, f(x), for all x in the domain. On the graph, this is the highest point when considering the entire function.

Can a point be both a global and a local extremum?

Yes, a point can be both a global and a local extremum. For example, if a point is the highest point of the entire function (global maximum) and also the highest point within a specific region (local maximum), it is both a global and local maximum. Similarly, a point can be both a global and local minimum if it is the lowest point of the entire function and within a specific region.

What is the convention for endpoints in determining extrema?

By the convention used in this course, endpoints can be considered global extrema but not local extrema. This means that an endpoint can be a global maximum or minimum if it is the highest or lowest point of the entire function. However, endpoints cannot be local extrema because they do not have nearby points on both sides to compare within a small region.

How do you determine a local minimum on a graph?

To determine a local minimum on a graph, you need to find a point where the function value, f(c), is less than or equal to all nearby function values, f(x). This point forms a valley in the graph and is lower than all other points in its immediate vicinity. It is the lowest point within a specific region of the function.