Choose a new eTextbook
Find eTextbooks for class
Search results for “{query}”
No results for “{query}”
0 results
Not finding your eTextbook? Search our complete catalog on pearson.com.
Explore our subjects
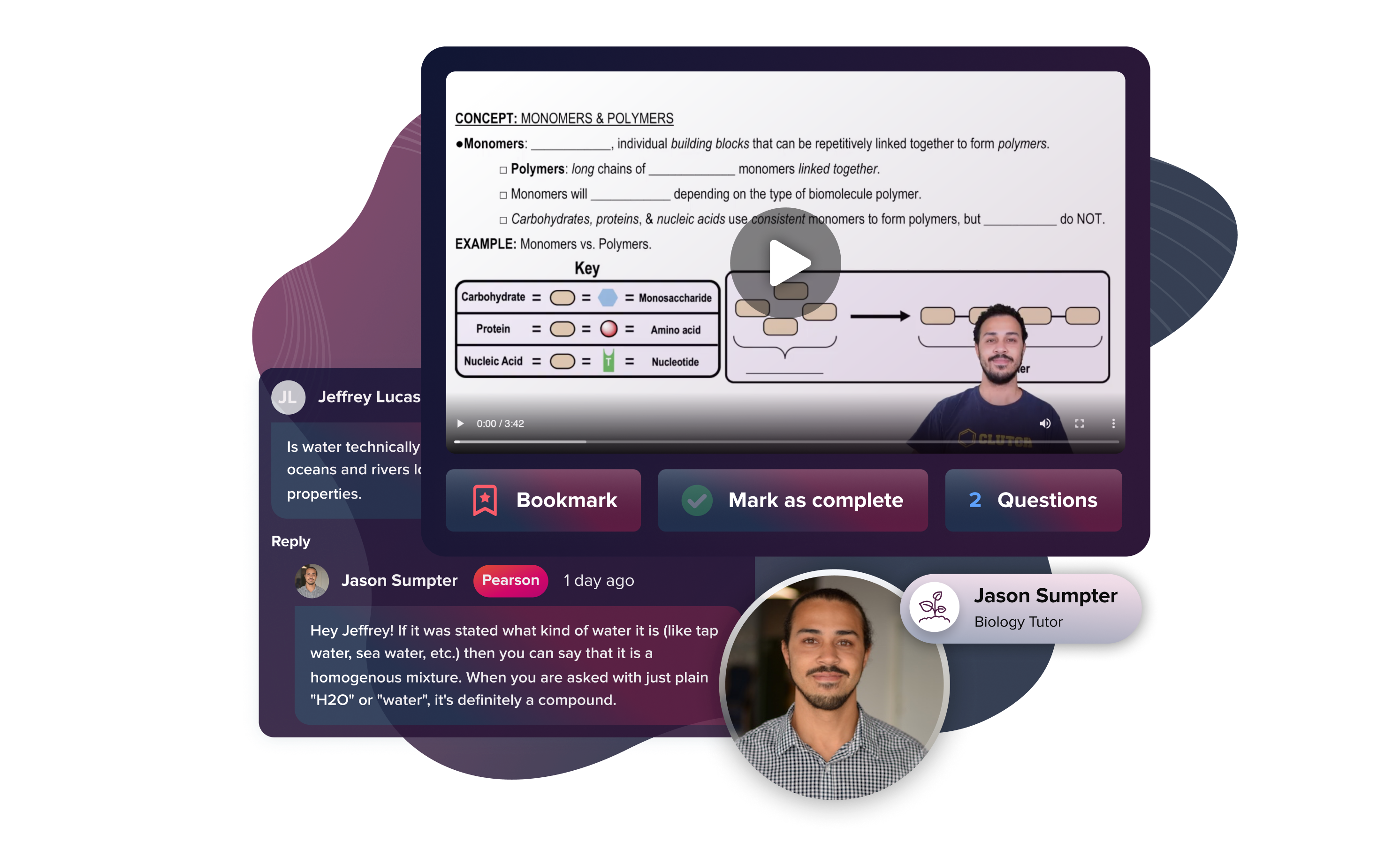
Get exam ready with Study Prep
Prepare for exams with videos and practice questions tailored to your course.