Use the law of sines to find the indicated part of each triangle ABC.
Find b if C = 74.2°, c = 96.3 m, B = 39.5
 Verified step by step guidance
Verified step by step guidance


Use the law of sines to find the indicated part of each triangle ABC.
Find b if C = 74.2°, c = 96.3 m, B = 39.5
CONCEPT PREVIEW Assume a triangle ABC has standard labeling.
a. Determine whether SAA, ASA, SSA, SAS, or SSS is given.
b. Determine whether the law of sines or the law of cosines should be used to begin solving the triangle.
a, b, and C
Find the magnitude and direction angle for each vector. Round angle measures to the nearest tenth, as necessary.
〈15, -8〉
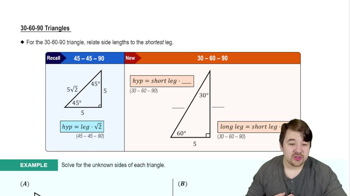
Find the length of each side labeled a. Do not use a calculator.
<IMAGE>
Find the magnitude and direction angle for each vector. Round angle measures to the nearest tenth, as necessary.
〈-4, 4√3〉
Refer to vectors a through h below. Make a copy or a sketch of each vector, and then draw a sketch to represent each of the following. For example, find a + e by placing a and e so that their initial points coincide. Then use the parallelogram rule to find the resultant, as shown in the figure on the right.
<IMAGE>
a + (b + c)