Here are the essential concepts you must grasp in order to answer the question correctly.
Trigonometric Identities
Trigonometric identities are equations that involve trigonometric functions and are true for all values of the variables involved. Common identities include the Pythagorean identities, reciprocal identities, and quotient identities. Understanding these identities is crucial for simplifying expressions and verifying equations in trigonometry.
Recommended video:
Fundamental Trigonometric Identities
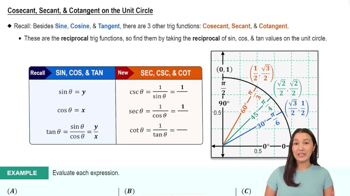
Reciprocal Functions
Reciprocal functions in trigonometry refer to pairs of functions where one function is the reciprocal of another. For example, the secant function (sec x) is the reciprocal of the cosine function (cos x), and the cosecant function (csc x) is the reciprocal of the sine function (sin x). Recognizing these relationships helps in transforming and simplifying trigonometric expressions.
Recommended video:
Secant, Cosecant, & Cotangent on the Unit Circle
Quotient Identity
The quotient identity in trigonometry states that the tangent function (tan x) is the ratio of the sine function (sin x) to the cosine function (cos x). This identity can be expressed as tan x = sin x / cos x. Understanding this identity is essential for verifying equations that involve tangent, as it allows for the substitution of sine and cosine functions.
Recommended video:
Quotients of Complex Numbers in Polar Form
 Verified step by step guidance
Verified step by step guidance