Graphing Other Common Polar Equations - Online Tutor, Practice Problems & Exam Prep

Understanding polar equations involves recognizing key shapes like cardioids, limacons, roses, and lemniscates. A cardioid is represented by $r^2=\pm a+bcos\theta$, while a limacon can have a dimple or inner loop based on the relationship between $a$ and $b$. Roses, defined by $r=acos(n\theta )$, exhibit petals based on the integer $n$. Lastly, lemniscates, shaped like an infinity symbol, are expressed as $r^2=\pm asin(2\theta )$.

Introduction to Common Polar Equations

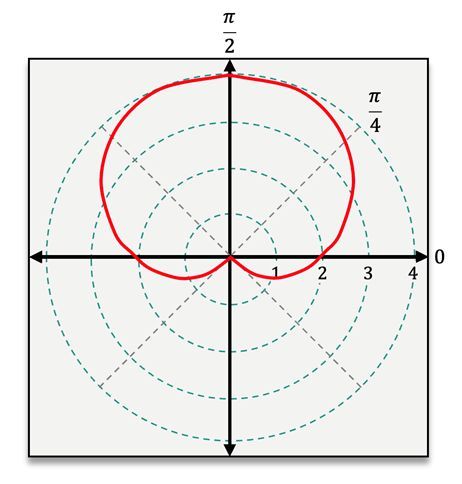
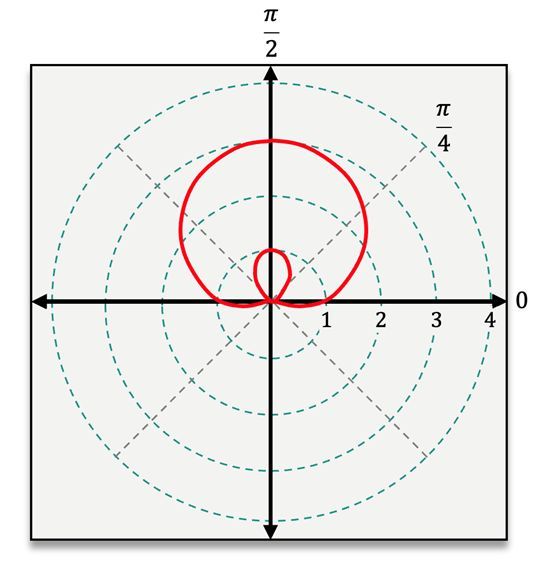
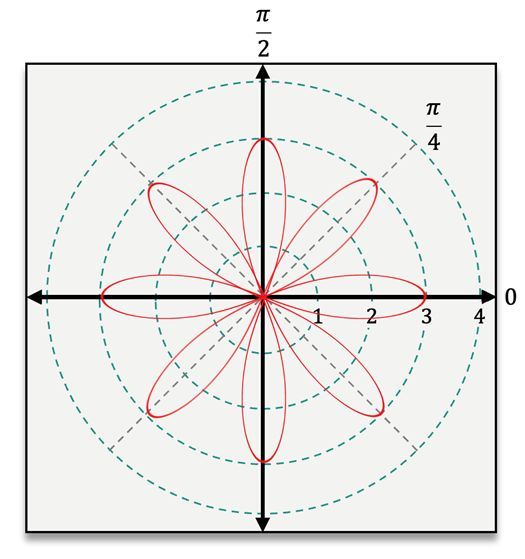
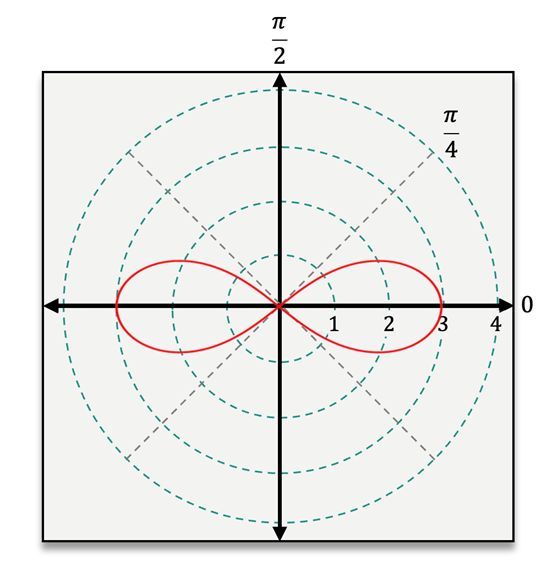
Hey everyone. When working with polar equations, there are 4 shapes that you'll encounter rather frequently. Now you're going to have to be able to recognize the equations for each of these in order to classify them and then also be able to graph them. Now here I'm going to break down for you the equations and the appearance of each of these commonly occurring shapes, and we'll work through classifying some equations together, laying the foundation to eventually be able to graph those equations as well. So let's go ahead and dive right in. Now looking at the equations for all of these shapes, they all look rather similar. They all contain an r, a theta, and a trig function. But let's actually dive into their differences here. Looking at our first two shapes, here we have the cardioid, named for its sort of resemblance to a heart shape, and the limacon. Now looking at the equations for these two shapes, you might notice that they're actually the exact same. They have identical equations. They're going to be of the form r=a±bcos(θ) or r=a±bsin(θ). Now the difference here is going to be with our a and b values. Now for the cardioid, a and b must both be greater than 0, but here, a is actually going to be equal to b. They're going to be the exact same value in order to get this cardioid shape. Now for the limacon, a and b are still going to be greater than 0, but a can either be greater than b or less than b, which affects the shape of our graph. If a is greater than b, then the graph of our limacon is just going to have a dimple at the top rather than the inner loop that we see in our graph here. But if a is less than b, that's when we get the inner loop that appears on our graph. Now the equations for cardioids and limacons are the only equations that are going to contain addition or subtraction. Now let's move on to our 3rd shape here, the rose, that looks like a sort of flower with a particular number of petals. Now the equation of a rose is going to be of the form r=a×cos(nθ) or r=a×sin(nθ). And for this equation, a cannot be equal to 0 and n is simply an integer that is greater than or equal to 2, which will actually end up telling us the number of petals that our rose has. Now let's move on to our final shape here, the lemniscate, which looks like a sort of infinity symbol. Now looking at our lemniscate here, the equation of a lemniscate is going to be of the form r2=±a2cos(2θ), or r2=±a2sin(2θ). Now here again, a cannot be equal to 0, and the equation of a lemniscate is actually going to be the only one that contains an r2, making it really easy to recognize these equations when they're going to have that lemniscate shape. Now that we've seen all of these equations for these commonly occurring shapes, let's go ahead and work through classifying some of them. Now looking at our first example here, we're given the equation r=1+cos(θ). Now here, since I have addition, I know that this equation is either that of a cardioid or a limacon. Now let's look at those a and b values. So here I have 1+cosine of theta, which has this sort of invisible one in front of it, telling me that a and b are both equal to 1. Now here, since a is equal to b, that means that this equation must be that of a cardioid. Now let's move on to our next equation here. Here we have r=4×sin(2θ). Now the first thing that I notice here is that I have this 2 theta in my argument, which is the same as that of a lemniscate. But the other thing that I notice here is that r is just r. It's not r squared, meaning that this cannot be the equation of a lemniscate. So it has to be that of a rose of the form r=a×sin(nθ), where n is equal to 2. So this is the equation of a rose. Now being able to classify these equations will allow us to immediately tell what the shape of the graph of that equation is going to be. So let's go ahead and keep that in mind as we continue to practice. Thanks for watching and I'll see you in the next one.

Identify whether the given equation is that of a cardioid, limaçon, rose, or lemniscate.

$r=4\sin2\theta$

• A. Cardioid
• B. Limacon
• C. Rose
• D. Lemniscate

Identify whether the given equation is that of a cardioid, limaçon, rose, or lemniscate.

$r=3+2\cos\theta$

• A. Cardioid
• B. Limacon
• C. Rose
• D. Lemniscate

Identify whether the given equation is that of a cardioid, limaçon, rose, or lemniscate.

$r^2=-25\cos2\theta$

• A. Cardioid
• B. Limacon
• C. Rose
• D. Lemniscate

Identify whether the given equation is that of a cardioid, limaçon, rose, or lemniscate.

$r=1-\sin\theta$

• A. Cardioid
• B. Limacon
• C. Rose
• D. Lemniscate

Cardioids

Hey, everyone. We're now familiar with the commonly occurring shapes that we'll encounter when graphing different polar equations, and now it's time to actually graph those shapes starting here with the cardioid. The general shape of the graph of our cardioid will remain the same with the orientation and positioning of it just changing based on the equation that we're actually graphing. Now remember that the equation of a cardioid will always be of the form r=a±bcos⁡θ or r=a±bsin⁡θ, where a=b. Now in order to actually graph a cardioid, we have only two things to determine. First, we want to determine the symmetry and then we simply want to plot points at our quadrantal angles. That's all. So let's go ahead and not waste any time here and just jump right into graphing this cardioid. We're tasked with graphing the equation, r=1+cos⁡β. I can tell that this is the graph of a cardioid because I have addition in this equation and this a value of 1 is equal to my b value of 1 because I have this sort of invisible one multiplying cos⁡θ. Jumping into our first step here in graphing this cardioid is to determine the symmetry. In order to determine the symmetry of a cardioid all we need to do is check whether our equation contains cosine or sine. Since our equation here is 1+cos⁡θ, that tells me that my graph will be symmetric about the polar axis, which is something that I should keep in mind as I continue into step 2 where we actually want to find and plot points at our quadrantal angles specifically. Remember that our quadrantal angles are 0, π/2, π, and 3π/2. Let's start here by plugging in θ=0 in order to find our r-value for this angle. Doing this, I get 1+cos⁡0, and the cosine of 0 is 1, so this ends up being 2. I can plot my first point at 2, 0, which will end up being right here on my graph. Now for my second quadrantal angle, π/2, plugging that into my equation, 1+cos⁡π/2, the cosine of π/2 is 0, so this r value is 1. I can plot my second point at 1, π/2, which will end up being right here. Then for my third quadrantal angle π, plugging in π to my equation 1+cos⁡π, the cosine of π is negative 1. So this ends up being 0. I can plot this point at 0, π, which will just end up being right at that pole because my r value is 0. Then for my final quadrantal angle 3π/2, I want to think back to my symmetry here. Because I know that my graph is symmetric about this polar axis, I can just take this point and reflect it right over that polar axis without having to calculate that value. So, that final point is going to be located at 1, 3π/2. Now we have all of these points and we can move on to our final step here which is going to be to connect everything with a smooth and continuous curve. We already know what the shape of our graph is. We know the general shape of a cardioid. And here we just want to apply that shape and connect all of these points here. Remember that a cardioid has sort of a bump at the top and then extends out. Our graph is going to end up looking like this. Remember that you can always calculate some more points if you want to get a bit more precise, but here we have fully graphed this cardioid. Now that we know how to graph cardioids, let's continue getting practice with this. Thanks for watching, and I'll see you in the next one.

Cardioids Example 1

In this problem, we're asked to graph r=2+2sin⁡(θ). Now I know that this is the graph of a cardioid because I have addition happening and both my a and b values are equal to each other. So, I already know the general shape of this graph and it remains to just determine the orientation and sort of the exact positioning of this on my graph. So let's go ahead and get started with step 1, first looking at symmetry. Now, since our equation contains a sine function, that tells me that my graph is going to be symmetric about the line θ=π/2, which we can keep in mind while graphing our points here.

Now we want to go ahead and find and plot some points, and we're specifically going to use our quadrantal angles starting, of course, with 0. So plugging in 0 for θ, I get 2+2sin⁡(0), which the sine of 0 is just 0, so this gives me 2. So I can plot that first point at 20, which will end up being right here. Now π/2, plugging that in for θ, I have 2+2⁡sin(π/2). Now the sine of π/2 is 1, so this ends up being 2 plus 2 or 4. So I can plot my second point at 4π/2. Now that will end up being right here at the top of that axis.

Now I want to take a moment to remember my symmetry here because since I'm symmetric about this line θ=π/2, I can go ahead and just reflect this point over onto my other quadrantal angle. So I have this other point at 2π. Then I have just one final point to find at 3π/2, so 2+2sin⁡(3π/2). The sine of 3π/2 is negative 1. So this ends up being 2 minus 2, which is just 0. So here my final point is actually going to be located at my pole. Now from here, we want to connect this with a smooth continuous curve. Now, we remember the shape of a cardioid, but remember that the orientation of that can change. Your furthest point from your pole will always be the sort of bottom of your cardioid that's very round. Then right here, we're going to have the sort of dimple heart shape that happens with our cardioid. And you want to make sure and round this around. Now it's okay if you don't get super precise. And you can always choose to plot some more points here if you want to get a bit more exact or if your professor asks you to get more exact. But this is the general shape and positioning of my cardioid for r=2+2sin⁡(θ).

Thanks for watching, and let me know if you have questions.

Graph $r=2-2\cos\theta$

• A.
• B.
• C.
• D.

Limacons

Hey, everyone. We can graph a limaçon just like we graphed a cardioid. By determining the symmetry of our graph and finding and plotting points at our quadrantal angles, we're just first going to take one additional step and determine whether our limaçon has a dimple or an inner loop, which we can do easily based on our a and b values given in our equation. So let's jump right into graphing our limaçon here. Remember that the equation of a limaçon will always be of the form r=a±bcos⁡(θ) or r=a±bsin⁡(θ), just like a cardioid, except here, a is either greater than or less than b. Now, the equation that we're tasked with graphing is r=3-2sin⁡(θ). I know that this is going to be the graph of a limaçon because I have subtraction happening here, and I have an a value of 3 and a b value of 2, so a is greater than b.

Now, this tells us that our limaçon will have a dimple rather than an inner loop. So, this tells me that my graph will be shaped something like this, and it's just up to us to get more precise with these other steps. Now, in determining whether our graph has a dimple or inner loop, we also learn some more information about our graph, whether or not it will pass through the pole. Since here our graph only has a dimple, it will not pass through the pole. So let's continue on with step 2 and determine the symmetry of our graph. Here our equation contains a sine function, so that tells us that our graph will be symmetric about the line theta=π/2, which again is something that I want to keep in mind as I move on to my next step where we're actually going to find and plot points at our quadrantal angles.

Now, for that first value of theta=0, I'm going to take 3 minus 2 sine of 0, and the sine of 0 is simply 0, so this will end up giving me a value of 3. I can plot that first point at (3, 0) right here. Then plugging in π/2 to my equation, 3 minus 2 times the sine of π/2, will give me a value of 1. So, I can plot this second point at (1, π/2) right here. Then, looking at this next angle, π, since I know that my graph is symmetric about this line, I can go ahead and just reflect this point over that line, in order to get this third point right here at (3, π). Now, for my final point plugging in 3/2π this gives me 3 minus 2 times the sine of 3/2π giving me a value of 5. So, this final point here is going to be located at (5, 3/2π), which will be right here.

Now, all that's left to do here is connect all of these points with a smooth and continuous curve and we know the general shape of the graph of a limaçon and, of course, that this limaçon has a dimple. So, in connecting these points, I want to make sure that I reflect those. Now here I'm going to go ahead and connect these points with a dimple at the top of my graph here, and my graph of this limaçon will end up looking something like this. Now, remember, if you're asked to get more precise or if you just want to get more precise, you can always plot more points and that's totally fine. But now that we have fully graphed this limaçon, let's continue getting some practice. Thanks for watching and I'll see you in the next one.

Limacons Example 2

Hey, everyone. In this problem, we're asked to graph the equation r=1+2cos⁡θ. Now, I know that this is a graph of a limaçon because I have addition happening and my a and b values are not equal to each other, therefore meaning that this cannot be a cardioid. Now, keeping in mind that this is the graph of a limaçon, let's go ahead and dive into our steps here. For our first step, we want to look at our a and b values. Now, I have an a=1, a b=2. Seeing that a is less than b, that tells me that my limaçon will have an inner loop rather than a dimple. If our limaçon has an inner loop, it also means that it will have a 0, which we can go ahead and plot on our graph here, right at our pole. Now, we can move on to step number 2 and determine our symmetry. Because our equation contains a cosine function, that tells us that our graph will be symmetric about the polar axis. This is something we want to keep in mind as we proceed to step 3 and actually start plotting some points. We want to plot our points using our quadrantal angles. So doing that here, I'm going to go ahead and plug in 0 for θ in my original equation, which is 1+2cos⁡θ, in this case 0. The cosine of 0 is 1, so this ends up being 3. So I'm going to plot my first point at 3, which is right here on that polar axis. Now, plugging in π/2, I get 1+2cos⁡π2. The cosine of π/2 is 0, so this ends up just being 1. I can go ahead and plot that point at 1 π/2, which will be right here. Now, remembering my symmetry here means that I can just reflect this point over the polar axis, giving me another point at my quadrantal angle of 3π/2 with an r value of 1. Now, we just need to plug in that π to get one final point here to get the complete picture of our graph. Now when I plug in π here, I get 1+2cos⁡π. The cosine of π is -1. So this will end up giving me 1 minus 2, which will give me -1. Now, remember when we have a negative r value, that means instead of counting out towards our angle, we want to count in the opposite direction. So that ends up giving me a point right here again on that polar axis. Now from here, we want to connect this with a smooth and continuous curve. Remembering back in step 1, we said that this limaçon has an inner loop. So what exactly does that look like? Well, it looks almost identical to the other limaçon, but now there's an extra little circle or loop in the middle. This point shows us what our inner loop is going to be, the point closest to the pole. So I have that inner loop right there. And then my outer loop, the rounded bottom of my limaçon, is going to be out here at the furthest point away from the pole, still having a curved line rounding around to that bottom point. This is the graph of my limaçon for the equation r=1+2cos⁡θ. Thanks for watching, and let me know if you have questions.

Graph $r=1+2\sin\theta$

• A.
• B.
• C.
• D.

Roses

Hey, everyone. We know that the general shape of the graph of a rose has these sort of petals. So it makes sense that in order to actually graph a rose, we need to be able to figure out how many petals our rose has and where exactly those petals are located. Now we can do this easily by just finding one single petal and then determining the spacing of our other petals, which we can do based on the equation that we're given. Now this is exactly what we're going to do here. So let's go ahead and jump right in. Now remember that the equation of a rose will always be of the form r=a⋅cos⁡ʃ⁡̨nΘ or r=a⋅sin⁡ʃ⁡̨nΘ, where a≠0 and n is an integer that is greater than or equal to 2.

The specific equation that we're tasked with graphing here is r=4⋅cos⁡ʃ2Θ, which I know is the graph of a rose because it's of this form, r=a⋅cos⁡ʃnΘ.

Now let's go ahead and get started with our very first step where we're going to look at our value of n. Now here n=2, and 2 is an even number. Now whenever n is even, that tells us that we're going to have 2n petals. So if I take 2 here and multiply it by my value of n, which is also 2, that tells me that this rose is going to have 4 petals.

Now with this in mind, let's move on to step 2 and figure out where that first petal is. Now in order to figure out where our first petal is, we need to look at our value of a. Now in my equation here, I see that a=4, so that tells me that my r value for my petal is going to be 4 and all of my petals will be at the same length. So, this will actually be the r value for every petal. Now we need to figure out what Θ is for this first petal, which is determined based on whether our equation contains cosine or sine. Here our equation contains a cosine, so that tells us that Θ here is going to be equal to 0. So, I can go ahead and plot that very first petal at 4,0, which will end up being right here.

Now we can move on to step number 3 because now that we have our first petal, we can determine where our other 3 petals are. That very first petal we know is located at 40. And we also know that all of those petals will be the exact same length. So I can go ahead and fill in 4 for all of those r values. Now I just need to figure out how these petals are spaced, which I can do based on the number of petals that we found in step 1. Now we found that our roses will have 4 petals. So here, if I take 2π and divide it by 4, that's how my petals will be spaced. Now this can simplify down to π 2 . So here, if I take this 0 of my first petal and add π 2 , that tells me that my second petal I can go ahead and plot at 4pi over 2, which is going to be right here. Then for my next petal, I'm going to add another pi over 2 to get me at pi. So I can plot my third petal here at 4pi, which will end up being right out here. Then for my final petal here, adding another pi over 2 for that spacing, I end up at 3pi over 2. And I can plot that very last petal at 4, 3pi over 2.

Now I have the positioning of all 4 of my petals. So all that's left to do is connect them with a smooth and continuous curve. Now I know that all of these petals will stem out from that pole because they're all coming kind of out of there to look like a flower. So my graph is going to end up looking something like this. Now again, remember, with all of these graphs, if you are asked to get more precise or if you want to get more precise, you can always calculate some more points, and that's totally fine. But now that we have fully graphed this rose, let's continue practicing graphing roses together. Thanks for watching, and I'll see you in the next one.

Roses Example 3

Hey, everyone. In this problem, we're asked to graph the equation \( r = 2 \times \sin(3\theta) \). Now, this is the equation of a rose of the form \( r = a \sin(n\theta) \). So let's go ahead and jump right into our steps here. For our first step, we're going to be looking at our value of \( n \), which in this case is 3. Remember, \( n \) is the number that comes before \( \theta \) in your argument. Now 3 is an odd number, so that tells us we're going to have \( n \) petals. In this case, \( n \) is 3, so we are going to have 3 petals.

Moving on to step 2, we want to actually plot our first petal. We know that we'll have 3 of them when we end up with our final graph, but we want to start by plotting that first one. In plotting our first petal, we need to look at our value of \( a \), which looking back at my equation I know is 2. \( A \) is the number that's at the front of your rose’s equation. So I have an \( a \) value of 2, and I want to figure out where \( \theta \) is going to be. Now because I have a sine function in my equation, \( \theta \) is going to be equal to \( \frac{\pi}{2} \times n \). So we have to do a little calculation here taking \( \pi \) and dividing it by \((2 \times n)\) which we know is 3 from step 1. Now this leaves me with an angle of \( \frac{\pi}{6} \), so my first petal is going to be graphed at \( 2 \times \frac{\pi}{6} \). Coming up to my angle \( \frac{\pi}{6} \) and going out to 2, I know that my first petal will be right here.

Now we can find our other petals by figuring out how far they are spaced out from each other and plotting all of them. I know that my first petal is located at \( 2 \times \frac{\pi}{6} \), but I have 2 other petals, so I need to figure out where those are. In order to figure out how far your petals are spaced apart, you're going to take \( 2\pi \) divided by the number of your petals, which in this case is 3. So these petals will be separated by \( \frac{2\pi}{3} \) radians. In order to determine where our next petal is, I need to take \( \frac{\pi}{6} \) and add \( \frac{2\pi}{3} \). When I do that, I'm going to end up getting \( \frac{5\pi}{6} \). All of my petals are the exact same length, so I can go ahead and fill in all of these \( r \) values as that \( a \) value of 2. So I can plot my second petal at \( \frac{5\pi}{6} \), which will end up being right out here on my graph. Then I have one other petal to account for, so I'm going to add another \( \frac{2\pi}{3} \) to that \( \frac{5\pi}{6} \). If you do this calculation, you're going to end up getting \( \frac{3\pi}{2} \). So I can plot my last petal at \( \frac{3\pi}{2} \), which will be right here.

Now we want to connect these with a smooth continuous curve. Remember that for roses, you're always going to go through the center; that's where your petals are kind of stemming out from. So we can go ahead and connect these with smooth continuous curves that look like petals because this is a rose. We're going to try our best to make these curves smooth, but if you don't get them exactly perfect, that's okay. This is the general shape of our graph for the rose \( r = 2 \times \sin(3\theta) \). Let me know if you have any questions.

Graph $r=3\cos4\theta$

• A.
• B.
• C.
• D.

Lemniscates

Hey, everyone. We know that the general shape of a lemniscate is this sort of infinity symbol or propeller shape with 2 petals. So in order to graph a lemniscate, if we just figured out where those 2 petals were, we'd be good to go. Now we can actually do this rather easily by just figuring out where our first petal is the same way we did for roses and then simply reflecting that petal over the pole. So let's not waste any time here and jump right into graphing our lemniscate. Now remember that the equation of a Lemniscate is always going to be of the form r2=±a2×cos(2θ) or a2×sin(2θ). Now here, the equation that we're specifically tasked with graphing is r2=4×sin(2θ). Now it's easy to tell that this is the equation of a lemniscate because it's the only polar equation that we're working with here that has a squared value of r.

So let's go ahead and jump into step number 1 and figure out where that very first petal is. Now, the first thing that we want to do here is look at our value of a. Now looking at my equation here, I have r2=4×sin(2θ). And something that's really important to remember here is that this 4 is not a. It's actually a2. So in order to get a, we need to take the square root of that 4 in order to get 2. So that tells us that our r value for that first petal is going to be 2. Now, in order to determine theta, we need to look at the sine of our equation and also whether we have a cosine or sine function. Here we have positive 4 sine of 2 theta. So that tells us we're dealing with a positive a2×sinθ, which means that theta will be equal to π4 for this first petal. I can go ahead and graph this first petal at 2π14, which will end up being right here.

Now all that's left to do is reflect this petal over the pole. Remember, my pole is what we think of as our origin in rectangular coordinates. So if I reflect this point over that pole, I'm going to end up down here for that second petal. Now all we have to do is connect these with a smooth and continuous curve, remembering that the shape of our lemniscate is a sort of infinity symbol. So let's go ahead and connect our points here. Coming out from the pole, I'm going to go out to that first point and then out to that second point. And here I have the graph of my lemniscate. Remember that if you're asked to get more precise or if you just want to get more precise, you can always calculate more points by plugging in values of theta to your equation. But now that we know how to graph a lemniscate, let's continue practicing together. Thanks for watching, and I'll see you in the next one.

Lemniscates Example 4

Hey, everyone. In this problem, we're asked to graph the equation r2=25⋅cos⁡2θ. Now here, this is the equation for a lemniscate because I have this r2, which I know is only something that happens when dealing with equations of lemniscates. Now lemniscates are arguably our easiest shape that we know how to graph, so let's dive right in here. Now looking at our first step, we want to plot our first petal here, which is going to be located at a for our r value, and then we need to determine what θ is based on the trig function that we're dealing with. Now remember that in our equation, this value at the beginning is actually a2. So we need to make sure that we take the square root of that in order to get a. Now the square root of 25 is equal to 5, so this gives me my value of a that I will be plotting for that first petal. Now we need to determine what θ is. Now here I have 25 times the cosine of 2 θ. So I'm dealing with a positive a2 and a cosine. So that tells me that θ will be located at 0. So I can plot my very first petal at 5 0 which will end up being right here on my polar axis. Now all that's left to do is reflect this petal over the pole. So doing that here, reflecting this over to the other side, landing me right here. I have my 2nd petal, and I can move on to my final step and just connect these with a smooth and continuous curve. Now we know that the general shape of our lemniscate is a sort of infinity symbol or a propeller or whatever you want to think about this as, but remember that we are always going to go to that hole in there with these sorts of petals or propellers or whatever you want to call these. Now we've graphed this lemniscate at r2=25⋅cos⁡2θ. Let me know if you have any questions.

Graph $r^2=9\sin2\theta$

• A.
• B.
• C.
• D.

Here’s what students ask on this topic:

What are the common shapes of polar equations and their corresponding forms?

Common shapes of polar equations include cardioids, limacons, roses, and lemniscates. A cardioid is represented by $r^2=\pm a+b\cos \theta$. Limacons can have a dimple or inner loop based on the relationship between $a$ and $b$. Roses, defined by $r=a\cos (n\theta )$, exhibit petals based on the integer $n$. Lastly, lemniscates, shaped like an infinity symbol, are expressed as $r^2=\pm a\sin (2\theta )$.

How do you determine the number of petals in a rose curve?

The number of petals in a rose curve is determined by the integer $n$ in the equation $r=a\cos (n\theta )$ or $r=a\sin (n\theta )$. If $n$ is even, the rose will have $2n$ petals. If $n$ is odd, the rose will have $n$ petals.

What is the difference between a cardioid and a limacon in polar equations?

A cardioid and a limacon both have equations of the form $r=a\pm b\cos (\theta )$ or $r=a\pm b\sin (\theta )$. The key difference is in the values of $a$ and $b$. For a cardioid, $a$ is equal to $b$. For a limacon, $a$ can be either greater than or less than $b$, resulting in a dimple or an inner loop.

How do you graph a lemniscate in polar coordinates?

To graph a lemniscate, start with the equation $r^2=\pm a{\cos }^{(}$ or $r^2=\pm a{\sin }^{(}$. Identify the value of $a$ by taking the square root of the constant term. Plot the first petal at $r$ equal to $a$ and $\theta$ equal to $\pi$ over 4. Reflect this petal over the pole to find the second petal. Connect the points with a smooth, continuous curve to form the infinity symbol shape.

How do you determine the symmetry of a polar graph?

To determine the symmetry of a polar graph, examine the equation. If the equation contains $\cos (\theta )$, the graph is symmetric about the polar axis. If it contains $\sin (\theta )$, the graph is symmetric about the line $\theta =\pi /2$. If the equation is unchanged when $\theta$ is replaced with $-\theta$, the graph is symmetric about the pole.