Hey, everyone. Welcome back. So we're going to spend a lot of time in this course talking about angles and triangles. And I want to give you a really good solid foundation for this because we'll be talking about them a lot later on. So in this video, I'm just going to walk you through a basic sort of refresher on the basics of triangles. There are a couple of important conceptual and mathematical things you need to know, and then we'll do some examples together. Let's get started here. A triangle is really just a geometric shape with three sides. That's a really sort of basic definition over here. All these things here have three sides, and they all sort of close together to form a shape, and that's a triangle. Now, there are actually three types of triangles that we can classify based on the lengths of their sides. This is just some vocabulary that you'll need to know. Alright? The first one is called an equilateral triangle, and this is where, if you'll see, all the lengths of the triangle are the same. All of them have a length of 3. Equilateral just means that three sides have equal length. That's actually what that word means. Alright? The way that we indicate this in diagrams is you'll see these little tick marks next to the numbers. That just means that those two or three measurements are all the same. That's an equilateral. An isosceles triangle is the next type, and this is where actually two of the side lengths have equal length. Notice how the bottom side is 3, and these two top sides over here are 5. That's an isosceles triangle. The last one is called a scalene triangle. This is where actually none of the sides have equal length. Notice how this is a 3, this is a 5, and this is a 6, so you'll see no tick marks anywhere. Another way of saying this is that all the sides are different in the scalene triangle. Alright? That's really all you need to know about their sides. Now, whenever sides meet in a triangle, they actually form angles. So the way we indicate this is by using a little curved arc symbol over here, and we express that angle in terms of degrees. So wherever you have two sides of a triangle meet, they form angles, and there are three other types of triangles that we can classify based on those angles. Alright. So again, this is just more vocabulary over here. An acute triangle over here is one in which all of the angles are less than 90 degrees. All of these words that you'll see acute, obtuse, and right have to do with what those angles are relative to 90. So look at these angles over here. All of these things are less than 90 degrees, so this is an acute triangle. Alright? So this next one over here, you'll see that there are two angles that measure 35 degrees, but there's one of them that measures 110. And this is an example of an obtuse triangle because one angle is greater than 90 degrees. So that's an obtuse triangle. The last one is called a right triangle. We're going to spend a lot of time talking about these, and these are special triangles where one of the angles is exactly equal to 90 degrees. Alright? Now, regardless of any type of triangle, whether we're looking at the sides or the angles, one really important thing you need to know is that in any type of triangle, all angles will always add up to 180 degrees. That is a fundamental property of triangles. So you would look at all of the triangles over here, all these three numbers will add up to 180. Same thing for this and same thing for this. Alright? So that's really important because if you know that all of the angles add up to 180, if you're ever missing one of them, then you can always find the other one. Alright? So that's actually really important. Let's go ahead and take a look at our first example over here. We're going to, for each of these triangles, figure out the missing angle or the missing side. Alright? So in this case, over here for this first example, we have a missing side represented by a variable over here. This is x. How do we find that? Well, we haven't discussed any mathematical ways of calculating this, but one of the things you can notice here is that these tick marks mean that the measurements have to be the same. So in other words, if the left side is 4, then that means that this also has to equal 4. Alright? So that's just something that you might need to know. Let's take a look at the next one, example b. This is one where we have two of the angles. This is 40 degrees, 40 degrees, but we're actually missing one of the other ones. How can I find that? Well, again, remember, all of the angles have to add up to 180 degrees in any triangle. So if you're ever missing one of them, you can always find the other. I'm just going to set up a simple equation over here. This is going to be 40 plus 40 plus theta. So, in other words, if I add up all of the angles, I have to get 180. If I just subtract 40 from both of the sides over here, this is basically the same thing as subtracting 80. What we're going to find here is that this angle is equal to 100 degrees. Alright? So this angle over here is 100 degrees, and therefore, this would actually be an obtuse triangle, but that's not what the question asked us. Alright? But that's the answer, theta equals 100. So that's it. That's just a basic introduction. Let's go ahead and get some practice.
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
Pythagorean Theorem & Basics of Triangles: Study with Video Lessons, Practice Problems & Examples
 Created using AI
Created using AIA triangle is a geometric shape with three sides, classified into equilateral, isosceles, and scalene based on side lengths, and acute, obtuse, and right based on angles. The fundamental property of triangles is that the sum of all angles equals 180 degrees. The Pythagorean theorem, \(a^2 + b^2 = c^2\), is essential for finding unknown sides in right triangles, where \(c\) is the hypotenuse. Understanding these concepts is crucial for solving various geometric problems and lays the groundwork for more advanced topics in mathematics.
Review of Triangles
Video transcript
Classify the triangle below according to its sides and angles.
I. Equilateral
II. Isosceles
III. Scalene
IV. Acute
V. Obtuse
VI. Right
I and IV
I and V
II and V
II and IV
III and VI
Only one of I, II, III, IV, V, and V
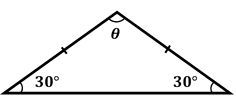
Find the missing angle θ for this right triangle.
30°
60°
90°
120°
Solving Right Triangles with the Pythagorean Theorem
Video transcript
Everyone, in a previous video, we discussed the basics of triangles, and I mentioned that we would very commonly be working with right triangles. But one of the most common situations that you'll see is where you have two sides of a right triangle that are known, but you have an unknown side. For example, we have 34 that are known here, but this side x here is missing. Well, don't worry because, in these kind of situations, we can always solve for this missing side by using something called the Pythagorean theorem. It's probably something that you've heard before in a math class, but we're going to be using it a lot in this course, and you'll need to know it. So I'm going to go ahead and explain it to you. What I'm going to show you is that it's really just an equation relating the three sides of a right triangle. Let's go ahead and get started. We'll do some examples together. Alright?
The first thing you need to know about the Pythagorean theorem is you can only use it when you have a right triangle. Alright? So you can only use it when you assume or know that one of the angles over here is 90 degrees. If you don't know that, then this equation won't work. So what is the equation? Well, it's really just a2+b2=c2. Again, you've probably heard that before, but it really means that if I take these two numbers over here, a and b, they'll just be numbers, and I square them and add them together, that's the same exact value as this side over here squared as well.
Let's take a look at our first example, so we can actually just get some practice with this and do it together. Alright? So we have 34 that are known over here, and you have x that's unknown. This is a right triangle, so I'll be able to use the Pythagorean theorem to solve that missing side. I just have my equation over here, a2+b2=c2. Alright?
So how does this work? Well, what's really, really important about the Pythagorean theorem as well is that you always have to keep in mind that your a and b need to be the shorter legs of the triangle. Always set your a and b as the shorter legs that form the corner, the 90-degree angle, and then you want to set c as the hypotenuse. The hypotenuse of a triangle is always the longest side, which usually is going to be the diagonal. Not always, but almost always. So in this right triangle over here, what we can see is that these two form the sort of corner like this, that's a and b, and c is going to be the diagonal, the longer one. That's what we set as c. Now, when it comes to a and b, it actually doesn't matter which one you pick as a or b.
So what this equation says is that a2+b2=c2. In other words, if I take 4 and square it, and I add it to 3 and square it, and I figure that out, that's going to give me this missing side squared. That's going to be x squared. Alright. So 422+322 actually just ends up being 16 plus 9. That's going to equal x squared. And if you actually just go ahead and work that out, that's going to be 25. So are we done here? Is the answer just 25?
Well, no. A lot of students will mess this up. You have one last step to do here, which is you have to take the square root of both sides because you want x, not x squared. If you do that, what you're going to get is that x is equal to 5, and that is the answer. So the hypotenuse of this triangle is equal to 5. Alright? One really quick way to check your work is to remember the hypotenuse has to be the longest side. So notice how 5 is longer than 3 and 4. If I got something that was lower than 3 or 4, then I know I would have messed something up.
Alright? But that's really all it is. Alright? That’s the Pythagorean theorem. Go ahead and pause the video and see if you can find the answer to this problem over here, example B. Alright? So let's go ahead and work it out.
So we've got this triangle over here. Notice how it's actually a little bit different because we have a right triangle just like we did over here. But this time, we actually know what the hypotenuse is. That diagonal longest side is something we already know. And, in fact, one of the shorter legs is actually one of our unknown values. But we can still use the Pythagorean theorem because remember, it's just we know 2 sides out of 3. I'm going to start off with my equation over here, a2+b2=c2. I set my c to be the hypotenuse. In other words, c is 10.
Again, it doesn't matter which one is my missing variable. Right? Or sorry, which one is my a and b. Either my a and b will just make up that 90-degree angle. So I'm just going to go ahead and set this one to be a and this one to be b. We'd get the exact same answer if you did it the other way. Alright? So this is b equals 6 and a equals 1. So what the Pythagorean theorem says is that a2+b2=c2. So in other words, y2+62=102. Now, you just plug in the values that you already know and calculate.
This is going to be y squared plus 36, that's 36 over here, that's going to equal 10 squared, which is 100. You can subtract 36 from both sides like this. Subtract 36. What you're going to get over here is that y squared is equal to 100 minus 36, which equals 64. That's equal 64. Now the last thing you have to do is just take the square root of both sides. You have y is equal to the square root of 64, and that's equal to 8.
So that is equal to 8 over here. So that means we go back into our diagram and this is going to equal 8. Notice how again, the hypotenuse, the 10 is still longer than both of the other shorter sides over here, and so that perfectly makes sense. Alright. So that's it for this one, folks. Thanks for watching and I'll see you in the next one.
Calculate the missing side of the triangle below.
9
25
19
15
Calculate the missing side of the triangle below.
Do you want more practice?
Here’s what students ask on this topic:
What are the different types of triangles based on their side lengths?
Triangles can be classified into three types based on their side lengths:
- Equilateral Triangle: All three sides are of equal length. Each angle in an equilateral triangle is 60 degrees.
- Isosceles Triangle: Two sides are of equal length, and the angles opposite these sides are equal.
- Scalene Triangle: All three sides are of different lengths, and all three angles are different.
 Created using AI
Created using AIHow do you classify triangles based on their angles?
Triangles can be classified into three types based on their angles:
- Acute Triangle: All three angles are less than 90 degrees.
- Obtuse Triangle: One angle is greater than 90 degrees.
- Right Triangle: One angle is exactly 90 degrees.
 Created using AI
Created using AIWhat is the Pythagorean theorem and how is it used?
The Pythagorean theorem is a fundamental principle in geometry that applies to right triangles. It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. The formula is:
where is the hypotenuse, and and are the other two sides. This theorem is used to find the length of an unknown side in a right triangle when the lengths of the other two sides are known.
 Created using AI
Created using AIHow do you find a missing angle in a triangle?
To find a missing angle in a triangle, you can use the fact that the sum of all angles in a triangle is always 180 degrees. If you know the measures of two angles, you can find the third angle by subtracting the sum of the known angles from 180 degrees. The formula is:
For example, if you have a triangle with angles of 40 degrees and 60 degrees, the missing angle would be:
 Created using AI
Created using AIWhat is the significance of the hypotenuse in a right triangle?
The hypotenuse is the longest side of a right triangle and is always opposite the right angle. It is significant because it is the side used in the Pythagorean theorem, which states:
where is the hypotenuse, and and are the other two sides. The hypotenuse is crucial for solving problems involving right triangles, such as finding the length of an unknown side.
 Created using AI
Created using AIYour Trigonometry tutors
- Fill in the blank(s) to correctly complete each sentence.The sum of the measures of the angles of any triangle...
- Fill in the blank(s) to correctly complete each sentence.An isosceles right triangle has one ________________ ...
- Fill in the blank(s) to correctly complete each sentence.An equilateral triangle has _________________ equal s...
- Find the measure of each marked angle. In Exercises 19–22, m and n are parallel. See Examples 1 and 2 .<IMA...
- Find the measure of each marked angle. In Exercises 19–22, m and n are parallel.<IMAGE>