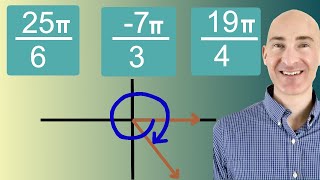
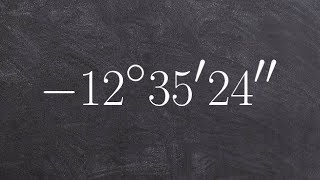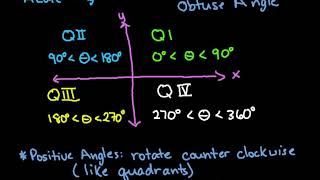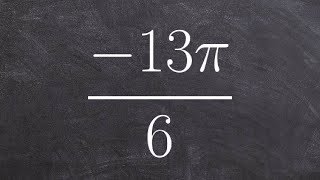1. Measuring Angles
Angles in Standard Position
1. Measuring Angles
Angles in Standard Position
Additional 7 creators.
Learn with other creators
Showing 10 of 10 videos
Practice this topic
- Multiple Choice
What is the approximate measure of the angle shown below? Choose the most reasonable answer.
739views6rank - Multiple Choice
Which angle is NOT a positive angle drawn in standard position?
664views4rank - Textbook QuestionIn Exercises 1–6, the measure of an angle is given. Classify the angle as acute, right, obtuse, or straight.135°625views
- Textbook QuestionIn Exercises 1–6, the measure of an angle is given. Classify the angle as acute, right, obtuse, or straight.87.177°488views
- Textbook QuestionIn Exercises 1–6, the measure of an angle is given. Classify the angle as acute, right, obtuse, or straight.𝜋531views1rank
- Textbook QuestionIn Exercises 1–6, the measure of an angle is given. Classify the angle as acute, right, obtuse, or straight.𝜋/2598views
- Multiple Choice
What is the angular position in radians of the minute hand of a clock at 3:30, measured from the 12 o'clock position in standard position (counterclockwise from the positive -axis)?
69views - Multiple Choice
If an angle in standard position measures , which of the following best describes its location on the coordinate plane?
73views