In Exercises 71–76, eliminate the parameter and graph the plane curve represented by the parametric equations. Use arrows to show the orientation of each plane curve. x = 3 + 2 cos t, y = 1+2 sin t; 0 ≤ t < 2π

Verified step by step guidance

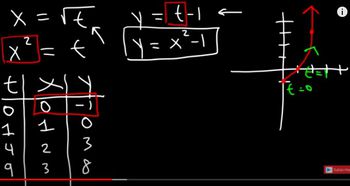
1. <Step 1: Identify the parametric equations.> The given parametric equations are $x = 3 + 2\cos t$ and $y = 1 + 2\sin t$. These equations describe a curve in the plane as the parameter $t$ varies from $0$ to $2\pi$.
2. <Step 2: Recognize the form of the equations.> Notice that the equations are in the form of a circle centered at $(h, k)$ with radius $r$. Specifically, $x = h + r\cos t$ and $y = k + r\sin t$. Here, $h = 3$, $k = 1$, and $r = 2$.
3. <Step 3: Eliminate the parameter $t$.> To eliminate $t$, use the trigonometric identities $\cos^2 t + \sin^2 t = 1$. Solve for $\cos t$ and $\sin t$ from the parametric equations: $\cos t = \frac{x - 3}{2}$ and $\sin t = \frac{y - 1}{2}$.
4. <Step 4: Substitute and simplify.> Substitute these expressions into the identity: $\left(\frac{x - 3}{2}\right)^2 + \left(\frac{y - 1}{2}\right)^2 = 1$. Simplify this equation to get the Cartesian equation of the circle.
5. <Step 5: Graph the circle and indicate orientation.> The resulting equation represents a circle centered at $(3, 1)$ with radius $2$. Graph this circle and use arrows to indicate the orientation, which is counterclockwise as $t$ increases from $0$ to $2\pi$.

Key Concepts

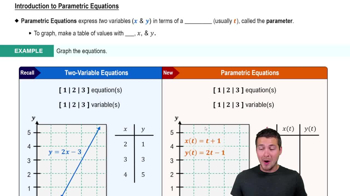
Parametric Equations

Parametric equations express the coordinates of points on a curve as functions of a variable, often denoted as 't'. In this case, x and y are defined in terms of the parameter t, which typically represents time or an angle. Understanding how to manipulate these equations is crucial for eliminating the parameter and finding a relationship between x and y.

Eliminating the Parameter

Eliminating the parameter involves finding a direct relationship between x and y without the parameter t. This is often done by solving one of the parametric equations for t and substituting it into the other equation. This process allows us to express the curve in Cartesian coordinates, making it easier to analyze and graph.

Graphing Plane Curves

Graphing plane curves requires understanding the shape and orientation of the curve based on the derived Cartesian equation. The orientation is indicated by arrows that show the direction of movement along the curve as the parameter t varies. Recognizing the type of curve (e.g., circle, ellipse) helps in accurately sketching the graph and understanding its properties.