Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
8. Vectors
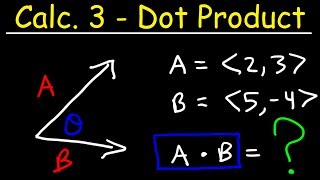
Dot Product
Problem 11
Textbook Question
In Exercises 9–16, let u = 2i - j, v = 3i + j, and w = i + 4j. Find each specified scalar. u ⋅ v + u ⋅ w
 Verified step by step guidance
Verified step by step guidance1
Step 1: Recall the formula for the dot product of two vectors \( \mathbf{a} \cdot \mathbf{b} = a_1b_1 + a_2b_2 \), where \( \mathbf{a} = a_1\mathbf{i} + a_2\mathbf{j} \) and \( \mathbf{b} = b_1\mathbf{i} + b_2\mathbf{j} \).
Step 2: Apply the dot product formula to find \( \mathbf{u} \cdot \mathbf{v} \). Here, \( \mathbf{u} = 2\mathbf{i} - \mathbf{j} \) and \( \mathbf{v} = 3\mathbf{i} + \mathbf{j} \). Calculate \( 2 \times 3 + (-1) \times 1 \).
Step 3: Apply the dot product formula to find \( \mathbf{u} \cdot \mathbf{w} \). Here, \( \mathbf{w} = \mathbf{i} + 4\mathbf{j} \). Calculate \( 2 \times 1 + (-1) \times 4 \).
Step 4: Add the results from Step 2 and Step 3 to find \( \mathbf{u} \cdot \mathbf{v} + \mathbf{u} \cdot \mathbf{w} \).
Step 5: Simplify the expression obtained in Step 4 to get the final scalar value.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Dot Product
The dot product is a fundamental operation in vector algebra that takes two vectors and returns a scalar. It is calculated by multiplying the corresponding components of the vectors and summing the results. For vectors u = ai + bj and v = ci + dj, the dot product is given by u ⋅ v = ac + bd. Understanding this concept is crucial for solving the given problem, as it involves calculating the dot products of the vectors u and v, and u and w.
Recommended video:

Introduction to Dot Product
Vector Components
Vectors can be expressed in terms of their components along the coordinate axes. In this case, the vectors u, v, and w are represented in a two-dimensional Cartesian coordinate system as u = 2i - j, v = 3i + j, and w = i + 4j. Recognizing the components of each vector allows for straightforward calculations of operations like the dot product, as each component corresponds to a specific direction in the plane.
Recommended video:

Position Vectors & Component Form
Scalar Addition
Scalar addition involves combining scalar quantities to produce a single scalar result. In the context of the problem, after calculating the dot products u ⋅ v and u ⋅ w, the next step is to add these two scalar results together. This concept is essential for arriving at the final answer, as it requires a clear understanding of how to manipulate and combine scalar values derived from vector operations.
Recommended video:

Multiplying Vectors By Scalars

 5:40m
5:40mWatch next
Master Introduction to Dot Product with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice