Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
5. Inverse Trigonometric Functions and Basic Trigonometric Equations
Linear Trigonometric Equations
Problem 123
Textbook Question
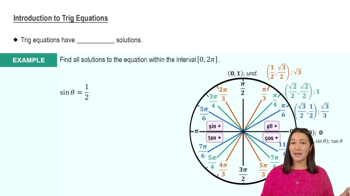
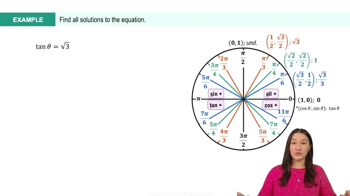
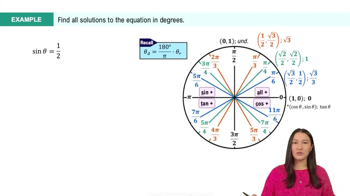
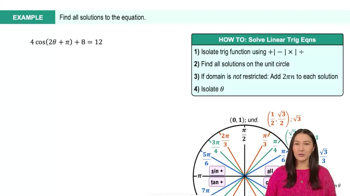
Textbook QuestionIn Exercises 121–126, solve each equation on the interval [0, 2𝝅). 10 cos² x + 3 sin x - 9 = 0
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
10mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Trigonometric Identities
Trigonometric identities are equations that involve trigonometric functions and are true for all values of the variables involved. Key identities include the Pythagorean identity (sin²x + cos²x = 1) and the double angle formulas. Understanding these identities is crucial for simplifying trigonometric equations and transforming them into a solvable form.
Recommended video:

Fundamental Trigonometric Identities
Quadratic Equations
A quadratic equation is a polynomial equation of the form ax² + bx + c = 0, where a, b, and c are constants. In the context of trigonometric equations, we often encounter quadratic forms in terms of sin x or cos x. Recognizing how to factor or apply the quadratic formula is essential for finding the solutions to these equations.
Recommended video:

Introduction to Quadratic Equations
Interval Notation
Interval notation is a mathematical notation used to represent a range of values. In this problem, the interval [0, 2π) indicates that we are looking for solutions within one full rotation of the unit circle, including 0 but excluding 2π. Understanding how to interpret and apply interval notation is important for determining valid solutions in trigonometric contexts.
Recommended video:

i & j Notation

 4:25m
4:25mWatch next
Master Introduction to Trig Equations with a bite sized video explanation from Callie Rethman
Start learning