Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
4. Graphing Trigonometric Functions
Graphs of the Sine and Cosine Functions
Problem 53a
Textbook Question
In Exercises 53–60, use a vertical shift to graph one period of the function. y = sin x + 2
 Verified step by step guidance
Verified step by step guidance1
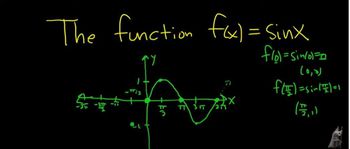
Identify the base function: The base function here is \( y = \sin x \).
Determine the vertical shift: The function \( y = \sin x + 2 \) indicates a vertical shift of 2 units upwards.
Graph the base function: Start by sketching the graph of \( y = \sin x \), which has a period of \( 2\pi \), an amplitude of 1, and oscillates between -1 and 1.
Apply the vertical shift: Shift the entire graph of \( y = \sin x \) upwards by 2 units. This means the new range of the function will be from 1 to 3.
Label key points: Mark the key points on the graph, such as the maximum, minimum, and intercepts, to reflect the vertical shift. For example, the maximum point at \( (\pi/2, 1) \) becomes \( (\pi/2, 3) \).
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Sine Function
The sine function, denoted as sin(x), is a periodic function that oscillates between -1 and 1. It represents the y-coordinate of a point on the unit circle as it rotates around the origin. Understanding its basic properties, such as amplitude, period, and phase shift, is essential for graphing transformations of the sine function.
Recommended video:

Graph of Sine and Cosine Function
Vertical Shift
A vertical shift involves moving the entire graph of a function up or down along the y-axis. For the function y = sin(x) + 2, the '+2' indicates a vertical shift of 2 units upward. This transformation affects the range of the function, changing it from [-1, 1] to [1, 3] for one period of the sine wave.
Recommended video:
Phase Shifts
Graphing Transformations
Graphing transformations involve altering the basic shape of a function through shifts, stretches, or reflections. In the case of y = sin(x) + 2, recognizing how vertical shifts affect the graph is crucial. By understanding these transformations, one can accurately sketch the modified sine wave and predict its behavior over one period.
Recommended video:

Introduction to Transformations

 5:53m
5:53mWatch next
Master Graph of Sine and Cosine Function with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice