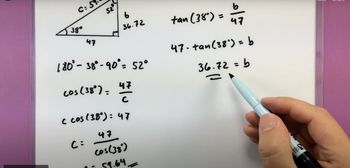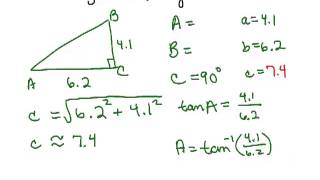Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
2. Trigonometric Functions on Right Triangles
Solving Right Triangles
Problem 37
Textbook Question
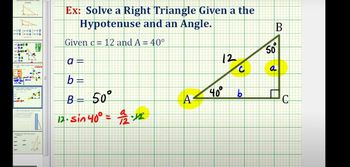
Textbook QuestionSolve each right triangle. In each case, C = 90°. If angle information is given in degrees and minutes, give answers in the same way. If angle information is given in decimal degrees, do likewise in answers. When two sides are given, give angles in degrees and minutes. See Examples 1 and 2. A = 53°24', c = 387.1 ft
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Right Triangle Properties
A right triangle has one angle measuring 90 degrees, and the other two angles must sum to 90 degrees. This property allows for the use of trigonometric ratios (sine, cosine, and tangent) to relate the angles to the lengths of the sides. Understanding these relationships is crucial for solving for unknown angles and sides in right triangles.
Recommended video:
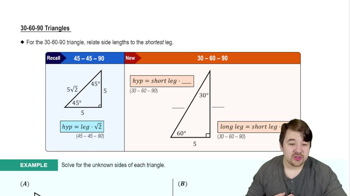
30-60-90 Triangles
Trigonometric Ratios
Trigonometric ratios are defined as the ratios of the lengths of the sides of a right triangle relative to its angles. For example, sine is the ratio of the opposite side to the hypotenuse, cosine is the adjacent side to the hypotenuse, and tangent is the opposite side to the adjacent side. These ratios are essential for calculating unknown angles and sides when given certain information.
Recommended video:

Introduction to Trigonometric Functions
Angle Measurement Conversions
Angles can be measured in degrees, minutes, and seconds or in decimal degrees. When solving problems involving angles, it is important to maintain consistency in the measurement format. Converting between these formats may be necessary, especially when given angles in degrees and minutes, to ensure accurate calculations and results.
Recommended video:

Reference Angles on the Unit Circle

 4:18m
4:18mWatch next
Master Finding Missing Side Lengths with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice