Find the indicated function value. If it is undefined, say so. See Example 4. sin 90°

Key Concepts

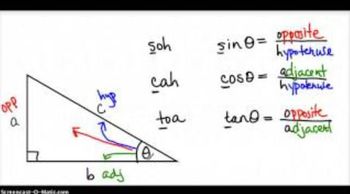
Sine Function

The sine function is a fundamental trigonometric function defined as the ratio of the length of the opposite side to the hypotenuse in a right triangle. It is commonly denoted as sin(θ), where θ is the angle in question. The sine function is periodic and varies between -1 and 1, with specific values at key angles such as 0°, 30°, 45°, 60°, and 90°.

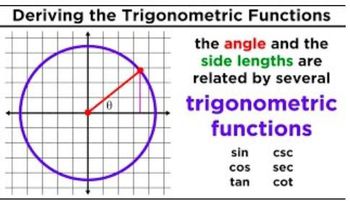
Unit Circle

The unit circle is a circle with a radius of one centered at the origin of a coordinate plane. It is a crucial tool in trigonometry for defining the sine, cosine, and tangent functions for all angles. The coordinates of points on the unit circle correspond to the cosine and sine values of the angle formed with the positive x-axis, making it easier to visualize and calculate trigonometric values.

Trigonometric Values at Key Angles

Trigonometric values at key angles (0°, 30°, 45°, 60°, and 90°) are essential for quickly determining sine, cosine, and tangent values without a calculator. For instance, sin(90°) equals 1, which represents the maximum value of the sine function. Understanding these key values allows for efficient problem-solving in trigonometry.