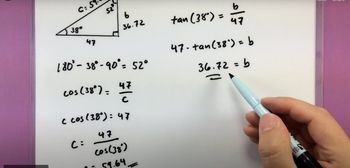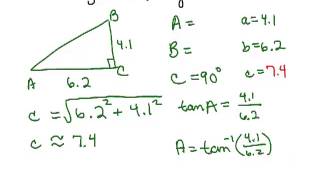Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
2. Trigonometric Functions on Right Triangles
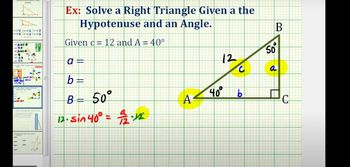
Solving Right Triangles
Problem 50
Textbook Question
Solve each problem. See Examples 1–4. Altitude of a Triangle Find the altitude of an isosceles triangle having base 184.2 cm if the angle opposite the base is 68°44'.
 Verified step by step guidance
Verified step by step guidance1
Convert the angle from degrees and minutes to decimal degrees. The angle is 68°44', which can be converted by adding 44/60 to 68.
Recognize that the altitude of the isosceles triangle forms two right triangles. The altitude is the opposite side to the angle at the base.
Use the trigonometric function tangent, which relates the opposite side (altitude) to the adjacent side (half of the base). The formula is: \( \tan(\theta) = \frac{\text{opposite}}{\text{adjacent}} \).
Calculate the adjacent side, which is half of the base: \( \frac{184.2}{2} \).
Rearrange the tangent formula to solve for the opposite side (altitude): \( \text{opposite} = \tan(\theta) \times \text{adjacent} \). Substitute the values to find the altitude.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
6mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Isosceles Triangle Properties
An isosceles triangle has two sides of equal length and two equal angles opposite those sides. The altitude from the vertex angle to the base bisects the base and creates two right triangles. Understanding these properties is essential for solving problems involving isosceles triangles, particularly when calculating heights or areas.
Recommended video:

Review of Triangles
Trigonometric Ratios
Trigonometric ratios, such as sine, cosine, and tangent, relate the angles of a triangle to the lengths of its sides. In this problem, the sine function can be used to find the altitude by relating it to the angle opposite the base and the length of the base. Mastery of these ratios is crucial for solving various triangle-related problems.
Recommended video:

Introduction to Trigonometric Functions
Angle Conversion
In trigonometry, angles can be expressed in degrees, minutes, and seconds or in decimal degrees. The angle given in the problem, 68°44', needs to be converted into decimal degrees for easier calculation with trigonometric functions. Understanding how to convert between these formats is important for accurate computations.
Recommended video:
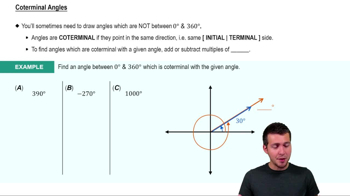
Coterminal Angles

 4:18m
4:18mWatch next
Master Finding Missing Side Lengths with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice