Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
2. Trigonometric Functions on Right Triangles
Trigonometric Functions on Right Triangles
Problem 33a
Textbook Question
Textbook QuestionSolve each problem. See Examples 3 and 4. Height of an Antenna A scanner antenna is on top of the center of a house. The angle of elevation from a point 28.0 m from the center of the house to the top of the antenna is 27°10', and the angle of elevation to the bottom of the antenna is 18°10'. Find the height of the antenna.
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
0m:0sPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Angle of Elevation
The angle of elevation is the angle formed by the horizontal line from an observer's eye to an object above that line. In this problem, it helps determine the height of the antenna by relating the observer's distance from the house and the angles to both the top and bottom of the antenna.
Recommended video:
Coterminal Angles
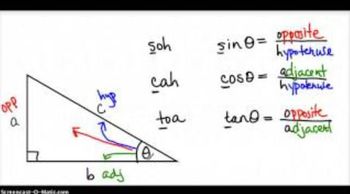
Trigonometric Ratios
Trigonometric ratios, such as sine, cosine, and tangent, relate the angles of a triangle to the lengths of its sides. In this scenario, the tangent function is particularly useful, as it connects the angle of elevation to the height of the antenna and the horizontal distance from the observer.
Recommended video:

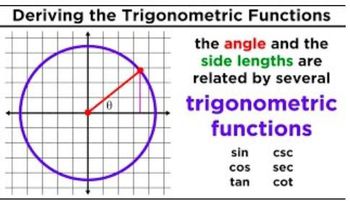
Introduction to Trigonometric Functions
Right Triangle Properties
The problem involves right triangles formed by the height of the antenna and the distance from the observer. Understanding the properties of right triangles, including how to apply the Pythagorean theorem and the relationships between angles and sides, is essential for calculating the height of the antenna accurately.
Recommended video:
30-60-90 Triangles

 6:4m
6:4mWatch next
Master Introduction to Trigonometric Functions with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice