Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
4. Graphing Trigonometric Functions
Graphs of the Sine and Cosine Functions
Problem 4.6
Textbook Question
Textbook QuestionFill in the blank(s) to correctly complete each sentence.
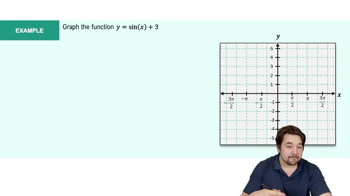
The graph of y = -5 + 2 cos x is obtained by shifting the graph of y = 2 cos x ________ unit(s) __________ (up/down).
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
0m:0sPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Cosine Function
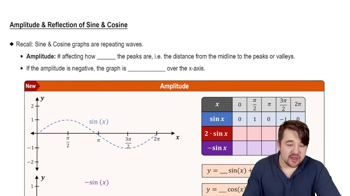
The cosine function, denoted as cos(x), is a fundamental trigonometric function that describes the relationship between the angle and the adjacent side of a right triangle. Its graph is a wave-like curve that oscillates between -1 and 1, with a period of 2π. Understanding the properties of the cosine function is essential for analyzing transformations such as shifts and stretches.
Recommended video:

Graph of Sine and Cosine Function
Vertical Shifts
Vertical shifts occur when a constant is added to or subtracted from a function, resulting in the entire graph moving up or down. For example, in the function y = 2 cos x, adding -5 shifts the graph down by 5 units. This concept is crucial for understanding how changes in the equation affect the position of the graph on the coordinate plane.
Recommended video:
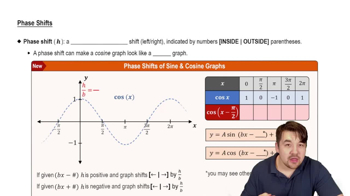
Phase Shifts
Transformations of Functions
Transformations of functions involve changes to the graph of a function, including shifts, stretches, and reflections. In the case of y = -5 + 2 cos x, the transformation includes a vertical shift and a vertical stretch. Recognizing these transformations helps in predicting how the graph will look based on modifications to the function's equation.
Recommended video:

Domain and Range of Function Transformations

 5:53m
5:53mWatch next
Master Graph of Sine and Cosine Function with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice