Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
2. Trigonometric Functions on Right Triangles
Trigonometric Functions on Right Triangles
Problem 28a
Textbook Question
Textbook QuestionSolve each problem. See Examples 1 and 2. Flying Distance The bearing from A to C is N 64° W. The bearing from A to B is S 82° W. The bearing from B to C is N 26° E. A plane flying at 350 mph takes 1.8 hr to go from A to B. Find the distance from B to C.
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
8mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Bearings
Bearings are a way of describing direction using angles measured clockwise from the north. In this problem, bearings such as N 64° W and S 82° W indicate specific angles relative to the north-south line, which are crucial for determining the relative positions of points A, B, and C in a coordinate system.
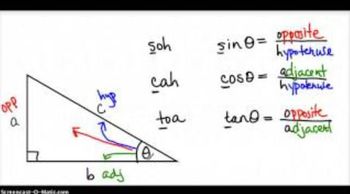
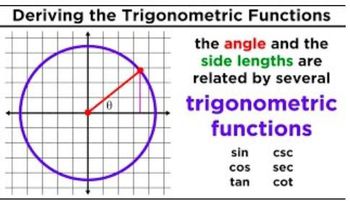
Trigonometric Functions
Trigonometric functions, such as sine, cosine, and tangent, relate the angles of a triangle to the lengths of its sides. These functions are essential for solving problems involving angles and distances, particularly when determining the distance from B to C using the angles derived from the bearings.
Recommended video:

Introduction to Trigonometric Functions
Distance and Speed Relationship
The relationship between distance, speed, and time is expressed by the formula distance = speed × time. In this scenario, knowing the speed of the plane and the time taken to travel from A to B allows us to calculate the distance AB, which can then be used in conjunction with the bearings to find the distance from B to C.
Recommended video:

Example 1

 6:4m
6:4mWatch next
Master Introduction to Trigonometric Functions with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice