Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
3. Unit Circle
Trigonometric Functions on the Unit Circle
Problem 69
Textbook Question
Textbook QuestionConcept Check Work each problem. What angle does the line y = √3x make with the positive x-axis?
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Slope of a Line
The slope of a line in the Cartesian plane is a measure of its steepness, calculated as the ratio of the rise (change in y) to the run (change in x). For the line given by the equation y = √3x, the slope is √3. This slope is crucial for determining the angle the line makes with the positive x-axis.
Recommended video:

Verifying Equations as Functions
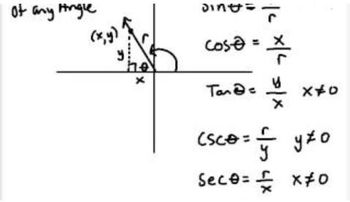
Tangent of an Angle
In trigonometry, the tangent of an angle in a right triangle is defined as the ratio of the length of the opposite side to the length of the adjacent side. The slope of a line can be interpreted as the tangent of the angle it makes with the x-axis. Therefore, to find the angle θ that the line y = √3x makes with the x-axis, we can use the relationship tan(θ) = slope.
Recommended video:

Inverse Tangent
Inverse Tangent Function
The inverse tangent function, denoted as arctan or tan⁻¹, is used to find an angle when the tangent value is known. Given the slope of the line (√3), we can find the angle θ by calculating θ = arctan(√3). This function is essential for converting the slope back into an angle measurement, which is necessary for answering the original question.
Recommended video:

Inverse Tangent

 6:34m
6:34mWatch next
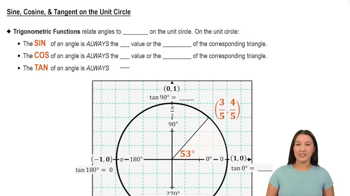
Master Sine, Cosine, & Tangent on the Unit Circle with a bite sized video explanation from Callie Rethman
Start learning