Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
0. Review of College Algebra
Basics of Graphing
Problem 8
Textbook Question
Textbook QuestionCONCEPT PREVIEW Fill in the blank(s) to correctly complete each sentence. The circle with equation x² + y² = 49 has center with coordinates ________ and radius equal to _______.
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Circle Equation
The standard equation of a circle in a Cartesian coordinate system is given by (x - h)² + (y - k)² = r², where (h, k) is the center of the circle and r is the radius. In this case, the equation x² + y² = 49 can be rewritten to identify the center and radius directly.
Recommended video:

Equations of Circles & Ellipses
Center of a Circle
The center of a circle is the point from which all points on the circle are equidistant. For the equation x² + y² = 49, the center is at the origin (0, 0) because there are no h or k values subtracted from x or y, indicating that the circle is centered at the coordinate axes.
Recommended video:

Introduction to the Unit Circle
Radius of a Circle
The radius of a circle is the distance from the center to any point on the circle. In the equation x² + y² = 49, the radius can be found by taking the square root of 49, which equals 7. Thus, the radius is 7 units.
Recommended video:

Introduction to the Unit Circle

 5:1m
5:1mWatch next
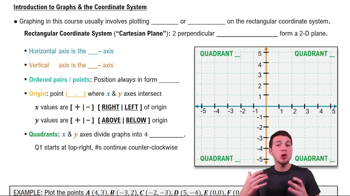
Master Introduction to Graphs & the Coordinate System with a bite sized video explanation from Patrick Ford
Start learning