CONCEPT PREVIEW Fill in the blank(s) to correctly complete each sentence. The point (-1, 3) lies in quadrant ________ in the rectangular coordinate system.

Key Concepts

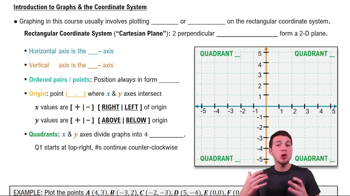
Quadrants in the Coordinate System

The rectangular coordinate system is divided into four quadrants based on the signs of the x and y coordinates. Quadrant I has positive x and y values, Quadrant II has negative x and positive y values, Quadrant III has negative x and y values, and Quadrant IV has positive x and negative y values. Understanding these quadrants is essential for determining the location of points in the plane.

Coordinate Points

A coordinate point is represented as an ordered pair (x, y), where 'x' indicates the horizontal position and 'y' indicates the vertical position on the coordinate plane. The first value corresponds to the x-coordinate, which determines the point's distance from the y-axis, while the second value corresponds to the y-coordinate, indicating its distance from the x-axis. This structure is fundamental for locating points in the coordinate system.

Sign of Coordinates

The sign of the coordinates (positive or negative) determines the quadrant in which a point lies. For example, a point with a negative x-coordinate and a positive y-coordinate, like (-1, 3), will be located in Quadrant II. Recognizing the significance of these signs is crucial for accurately identifying the position of points in the coordinate system.