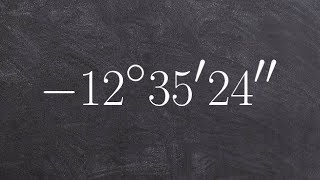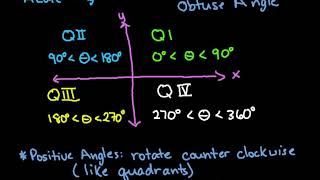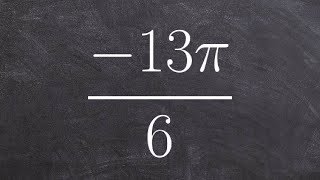Table of contents
- 0. Review of College Algebra4h 43m
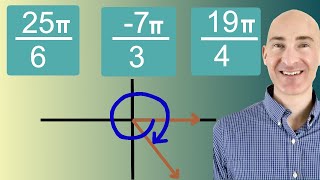
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
1. Measuring Angles
Angles in Standard Position
Problem 91
Textbook Question
Textbook Question(Modeling) Length of a Sag Curve When a highway goes downhill and then uphill, it has a sag curve. Sag curves are designed so that at night, headlights shine sufficiently far down the road to allow a safe stopping distance. See the figure. S and L are in feet. The minimum length L of a sag curve is determined by the height h of the car's headlights above the pavement, the downhill grade θ₁ < 0°, the uphill grade θ₂ > 0°, and the safe stopping distance S for a given speed limit. In addition, L is dependent on the vertical alignment of the headlights. Headlights are usually pointed upward at a slight angle α above the horizontal of the car. Using these quantities, for a 55 mph speed limit, L can be modeled by the formula (θ₂ - θ₁)S² L = ————————— , 200(h + S tan α) where S < L. (Data from Mannering, F., and W. Kilareski, Principles of Highway Engineering and Traffic Analysis, Second Edition, John Wiley and Sons.) Compute length L, to the nearest foot, if h = 1.9 ft, α = 0.9°, θ₁ = -3°, θ₂ = 4°, and S = 336 ft.
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
0m:0sPlay a video:
21
views
Was this helpful?
Video transcript
Related Videos
Related Practice