Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
1. Measuring Angles
Complementary and Supplementary Angles
Problem 68
Textbook Question
Textbook QuestionIn Exercises 67–68, an object is attached to a coiled spring. In Exercise 67, the object is pulled down (negative direction from the rest position) and then released. In Exercise 68, the object is propelled downward from its rest position. Write an equation for the distance of the object from its rest position after t seconds.
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Simple Harmonic Motion
Simple Harmonic Motion (SHM) describes the oscillatory motion of an object attached to a spring, where the restoring force is proportional to the displacement from its equilibrium position. This motion can be modeled using sine or cosine functions, which represent the periodic nature of the oscillation. Understanding SHM is crucial for deriving the equations that describe the distance of the object from its rest position over time.
Recommended video:

Products of Complex Numbers in Polar Form
Differential Equations
Differential equations are mathematical equations that relate a function to its derivatives. In the context of SHM, they can be used to model the motion of the spring system, leading to equations that describe the position of the object as a function of time. Solving these equations helps in determining the specific form of the distance equation based on initial conditions, such as the initial displacement and velocity.
Recommended video:

Parameterizing Equations
Phase Shift
Phase shift refers to the horizontal shift in the graph of a periodic function, such as sine or cosine. In the context of the problem, the initial conditions of the object's motion (whether it is pulled down or propelled downward) will affect the phase of the resulting trigonometric function. Understanding phase shifts is essential for accurately writing the equation that represents the distance of the object from its rest position after a given time.
Recommended video:
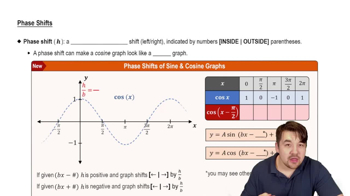
Phase Shifts

 3:35m
3:35mWatch next
Master Intro to Complementary & Supplementary Angles with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice








