Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
3. Unit Circle
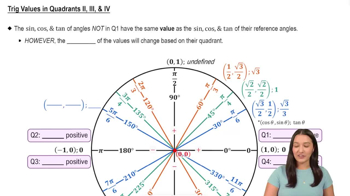
Reference Angles
Problem 55
Textbook Question
Textbook QuestionIn Exercises 49–59, find the exact value of each expression. Do not use a calculator. sin(-𝜋/3)
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Unit Circle
The unit circle is a circle with a radius of one centered at the origin of a coordinate plane. It is fundamental in trigonometry as it provides a geometric interpretation of the sine, cosine, and tangent functions. The coordinates of points on the unit circle correspond to the cosine and sine values of angles measured from the positive x-axis, allowing for easy calculation of trigonometric values.
Recommended video:

Introduction to the Unit Circle
Sine Function
The sine function, denoted as sin(θ), represents the y-coordinate of a point on the unit circle corresponding to an angle θ. It is periodic with a period of 2π, meaning that sin(θ) = sin(θ + 2nπ) for any integer n. Understanding the sine function's behavior, including its values for common angles, is crucial for evaluating expressions like sin(-π/3).
Recommended video:

Graph of Sine and Cosine Function
Negative Angles
In trigonometry, negative angles indicate a clockwise rotation from the positive x-axis. The sine function is an odd function, which means that sin(-θ) = -sin(θ). This property simplifies the evaluation of sine for negative angles, allowing us to find sin(-π/3) by using the positive angle equivalent, leading to the conclusion that sin(-π/3) = -sin(π/3).
Recommended video:
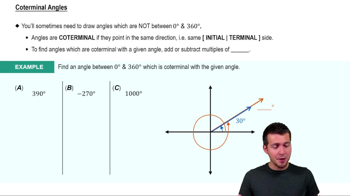
Coterminal Angles

 5:31m
5:31mWatch next
Master Reference Angles on the Unit Circle with a bite sized video explanation from Callie Rethman
Start learningRelated Videos
Related Practice