Concept Check Match each angle in Column I with its reference angle in Column II. Choices may be used once, more than once, or not at all. See Example 1. I. II. 5. A. 45° 6. 212° B. 60° 7. C. 82° 8. D. 30° 9. E. 38° 10. F. 32°

Key Concepts

Reference Angle

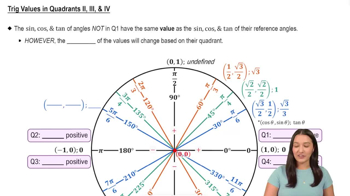
A reference angle is the acute angle formed by the terminal side of an angle in standard position and the x-axis. It is always measured as a positive angle and is used to simplify the analysis of angles in different quadrants. For example, the reference angle for 212° is found by subtracting it from 360° or determining its equivalent acute angle.

Quadrants of the Unit Circle

The unit circle is divided into four quadrants, each representing a range of angles. The first quadrant contains angles from 0° to 90°, the second from 90° to 180°, the third from 180° to 270°, and the fourth from 270° to 360°. Understanding which quadrant an angle lies in helps in determining its reference angle and associated trigonometric values.

Angle Measurement

Angles can be measured in degrees or radians, with degrees being the more common unit in basic trigonometry. A full rotation is 360°, and angles can be positive (counterclockwise) or negative (clockwise). Recognizing how to convert between degrees and radians is essential for solving problems involving angles and their reference angles.