Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
3. Unit Circle
Reference Angles
Problem 68
Textbook Question
Textbook QuestionFind all values of θ, if θ is in the interval [0°, 360°) and has the given function value. See Example 6. √3 sin θ = - —— 2
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
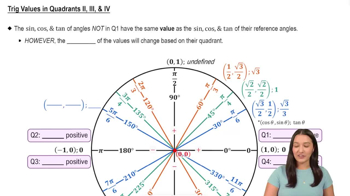
Understanding the Unit Circle
The unit circle is a fundamental concept in trigonometry that defines the relationship between angles and the coordinates of points on the circle. Angles are measured from the positive x-axis, and the sine and cosine of an angle correspond to the y and x coordinates of a point on the circle, respectively. This understanding is crucial for determining the values of θ that satisfy trigonometric equations.
Recommended video:

Introduction to the Unit Circle
Sine Function and Its Values
The sine function, denoted as sin(θ), represents the ratio of the length of the opposite side to the hypotenuse in a right triangle. It is periodic and takes values between -1 and 1. In this problem, we need to find angles θ where sin(θ) equals a specific negative value, which indicates that θ must be in the third or fourth quadrants of the unit circle.
Recommended video:

Sine, Cosine, & Tangent of 30°, 45°, & 60°
Solving Trigonometric Equations
Solving trigonometric equations involves finding all angles that satisfy a given equation within a specified interval. This often requires using inverse trigonometric functions and understanding the periodic nature of trigonometric functions. In this case, we will find the reference angle for sin(θ) = -√3/2 and then determine the corresponding angles in the appropriate quadrants.
Recommended video:

How to Solve Linear Trigonometric Equations

 5:31m
5:31mWatch next
Master Reference Angles on the Unit Circle with a bite sized video explanation from Callie Rethman
Start learningRelated Videos
Related Practice