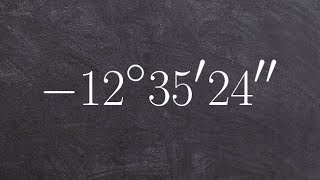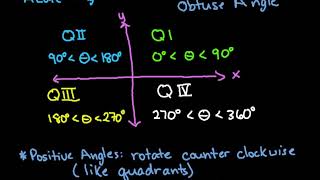Find the angle of least positive measure (not equal to the given measure) that is coterminal with each angle. See Example 5. 1000°

Verified step by step guidance

1. Convert the given angle from degrees to a standard angle by finding its equivalent within the range of 0° to 360°.
2. To do this, subtract 360° from the given angle repeatedly until the result is within the range of 0° to 360°.
3. Alternatively, you can use the modulo operation: find 1000° mod 360° to get the equivalent angle within the standard range.
4. Once you have the equivalent angle, check if it is the least positive measure. If it is not, add 360° to the result to find the next coterminal angle.
5. Verify that the new angle is the least positive measure that is coterminal with the original angle.

Key Concepts

Coterminal Angles

Coterminal angles are angles that share the same terminal side when drawn in standard position, differing only by full rotations of 360 degrees. To find a coterminal angle, you can add or subtract multiples of 360° from the given angle. For example, 1000° and 280° are coterminal because 1000° - 2(360°) = 280°.

Finding Positive Angles

When tasked with finding the least positive coterminal angle, the goal is to ensure the resulting angle is greater than 0° but less than 360°. This often involves subtracting 360° from the original angle until the result falls within the desired range. This process helps in identifying the smallest positive angle that is coterminal with the given angle.

Angle Measurement

Angles can be measured in degrees or radians, with degrees being the more common unit in basic trigonometry. A full rotation is 360°, and understanding this measurement is crucial for determining coterminal angles. In this context, recognizing how to convert and manipulate angles within the degree system is essential for solving the problem effectively.