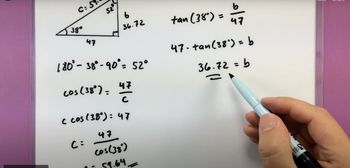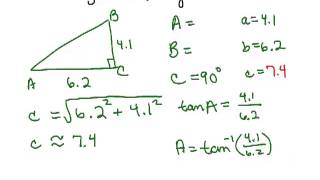Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
2. Trigonometric Functions on Right Triangles
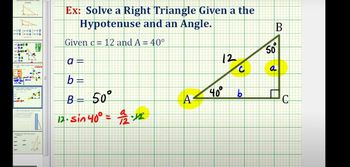
Solving Right Triangles
Problem 8
Textbook Question
Textbook QuestionConcept Check Refer to the discussion of accuracy and significant digits in this section to answer the following. Mt. Everest When Mt. Everest was first surveyed, the surveyors obtained a height of 29,000 ft to the nearest foot. State the range represented by this number. (The surveyors thought no one would believe a measurement of 29,000 ft, so they reported it as 29,002.) (Data from Dunham, W., The Mathematical Universe, John Wiley and Sons.)
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Significant Digits
Significant digits, or significant figures, are the digits in a number that contribute to its precision. This includes all non-zero digits, any zeros between significant digits, and trailing zeros in the decimal portion. In the context of the Mt. Everest measurement, the reported height of 29,000 ft indicates that the measurement is precise to the nearest foot, meaning the actual height could range from 28,999.5 ft to 29,000.5 ft.
Measurement Range
The measurement range refers to the interval within which the true value of a measurement is expected to lie, based on the precision indicated by significant digits. For the height of Mt. Everest reported as 29,000 ft, the range can be calculated by considering the rounding to the nearest foot, which results in a range of 28,999.5 ft to 29,000.5 ft. This range reflects the uncertainty inherent in the measurement process.
Recommended video:

Domain and Range of Function Transformations
Rounding and Reporting
Rounding is the process of adjusting a number to a specified degree of precision, often to make it easier to work with or to reflect the accuracy of the measurement. In this case, the surveyors rounded the height of Mt. Everest to 29,000 ft, but they also reported it as 29,002 ft to enhance credibility. This highlights the importance of how measurements are communicated and the potential implications for accuracy and perception.
Recommended video:

How to Use a Calculator for Trig Functions

 4:18m
4:18mWatch next
Master Finding Missing Side Lengths with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice