Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
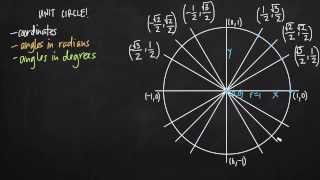
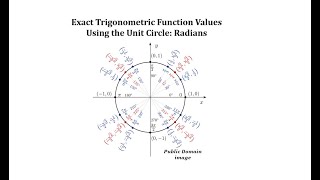
3. Unit Circle
Defining the Unit Circle
Problem 3.43b
Textbook Question
Find a calculator approximation to four decimal places for each circular function value. See Example 3.
cot 6.0301
 Verified step by step guidance
Verified step by step guidance1
Understand that \( \cot \theta = \frac{1}{\tan \theta} \). Therefore, to find \( \cot 6.0301 \), you need to first find \( \tan 6.0301 \).
Use a calculator to find \( \tan 6.0301 \). Make sure your calculator is set to the correct mode (radians or degrees) based on the context of the problem.
Once you have \( \tan 6.0301 \), calculate \( \cot 6.0301 \) by taking the reciprocal: \( \cot 6.0301 = \frac{1}{\tan 6.0301} \).
Use the calculator to compute the reciprocal value to get \( \cot 6.0301 \).
Round the result to four decimal places as required.
Was this helpful?

 6:11m
6:11mWatch next
Master Introduction to the Unit Circle with a bite sized video explanation from Callie Rethman
Start learningRelated Videos
Related Practice