Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
3. Unit Circle
Trigonometric Functions on the Unit Circle
Problem 3.81
Textbook Question
Textbook QuestionSuppose an arc of length s lies on the unit circle x² + y² = 1, starting at the point (1, 0) and terminating at the point (x, y). (See Figure 12, repeated below.) Use a calculator to find the approximate coordinates for (x, y) to four decimal places.
s = ―7.4
<IMAGE>
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
0m:0sPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Unit Circle
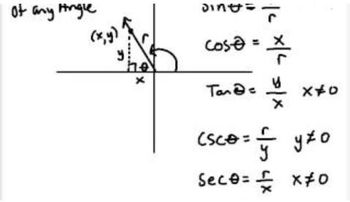
The unit circle is a circle with a radius of one centered at the origin of a coordinate plane. It is a fundamental concept in trigonometry, as it provides a geometric representation of the sine and cosine functions. Any point (x, y) on the unit circle corresponds to the cosine and sine of an angle θ, where x = cos(θ) and y = sin(θ). Understanding the unit circle is essential for solving problems involving angles and arc lengths.
Recommended video:

Introduction to the Unit Circle
Arc Length
Arc length is the distance along the curve of a circle between two points. For a unit circle, the arc length s can be calculated using the formula s = rθ, where r is the radius and θ is the angle in radians. Since the radius of the unit circle is 1, the arc length is directly equal to the angle in radians. This relationship is crucial for determining the coordinates of points on the circle based on a given arc length.
Recommended video:

Finding Missing Side Lengths
Radians and Degrees
Radians and degrees are two units for measuring angles. One complete revolution around a circle is 360 degrees or 2π radians. Radians are often preferred in trigonometry because they provide a direct relationship between the angle and the arc length on the unit circle. Converting between these units is essential when calculating angles or arc lengths, especially when using a calculator to find coordinates based on a specified arc length.
Recommended video:

Converting between Degrees & Radians

 6:34m
6:34mWatch next
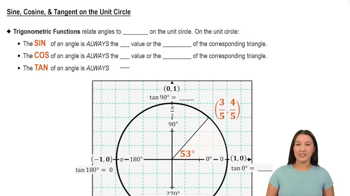
Master Sine, Cosine, & Tangent on the Unit Circle with a bite sized video explanation from Callie Rethman
Start learning