In Exercises 35–60, find the reference angle for each angle. 160°

Key Concepts

Reference Angle

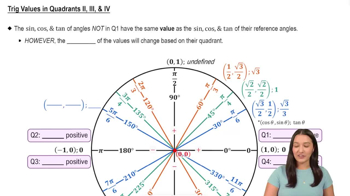
The reference angle is the acute angle formed by the terminal side of a given angle and the x-axis. It is always measured as a positive angle and is typically between 0° and 90°. For angles greater than 180°, the reference angle can be found by subtracting the angle from 360° or by using the appropriate quadrant's properties.

Quadrants of the Coordinate Plane

The coordinate plane is divided into four quadrants, each defined by the signs of the x and y coordinates. The first quadrant (0° to 90°) has both coordinates positive, the second (90° to 180°) has a positive y and negative x, the third (180° to 270°) has both negative, and the fourth (270° to 360°) has a positive x and negative y. Understanding these quadrants is essential for determining the reference angle.

Angle Measurement

Angles can be measured in degrees or radians, with 360° equivalent to 2π radians. In this context, angles greater than 180° need to be converted to their reference angles by considering their position relative to the x-axis. For example, an angle of 160° is in the second quadrant, and its reference angle is found by subtracting it from 180°.