Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
5. Inverse Trigonometric Functions and Basic Trigonometric Equations
Linear Trigonometric Equations
Problem 65b
Textbook Question
In Exercises 54–67, solve each equation on the interval [0, 2𝝅). Use exact values where possible or give approximate solutions correct to four decimal places. 5 cos² x - 3 = 0
 Verified step by step guidance
Verified step by step guidance1
Start by isolating the trigonometric function. Add 3 to both sides of the equation to get: \(5 \cos^2 x = 3\).
Divide both sides by 5 to solve for \(\cos^2 x\): \(\cos^2 x = \frac{3}{5}\).
Take the square root of both sides to solve for \(\cos x\): \(\cos x = \pm \sqrt{\frac{3}{5}}\).
Determine the angles \(x\) in the interval \([0, 2\pi)\) that satisfy \(\cos x = \sqrt{\frac{3}{5}}\) and \(\cos x = -\sqrt{\frac{3}{5}}\).
Use the unit circle or inverse cosine function to find the exact or approximate values of \(x\) for each case.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
7mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Trigonometric Identities
Trigonometric identities are equations that involve trigonometric functions and are true for all values of the variable. In this case, the identity cos² x = 1 - sin² x can be useful for transforming the equation into a more manageable form. Understanding these identities is crucial for simplifying and solving trigonometric equations.
Recommended video:

Fundamental Trigonometric Identities
Solving Quadratic Equations
The equation 5 cos² x - 3 = 0 is a quadratic equation in terms of cos x. To solve it, one can rearrange it into standard form and apply methods such as factoring, completing the square, or using the quadratic formula. Recognizing the structure of the equation as quadratic is essential for finding the solutions.
Recommended video:

Solving Quadratic Equations by Completing the Square
Interval Notation
Interval notation specifies the range of values for which the solutions are valid. In this problem, the interval [0, 2π) indicates that solutions must be found within one full rotation of the unit circle, from 0 to just below 2π. Understanding how to interpret and apply interval notation is important for ensuring that all solutions are within the specified range.
Recommended video:

i & j Notation

 4:25m
4:25mWatch next
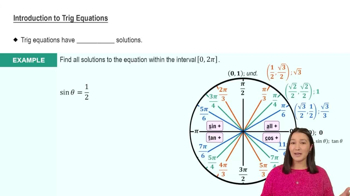
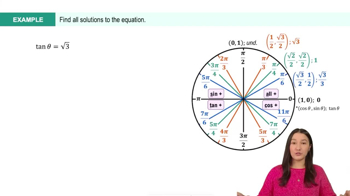
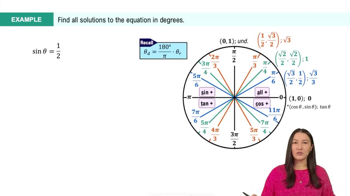
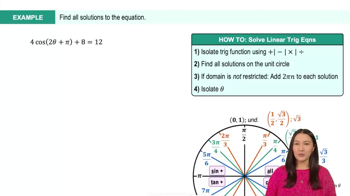
Master Introduction to Trig Equations with a bite sized video explanation from Callie Rethman
Start learning