Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
3. Unit Circle
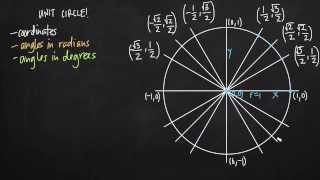
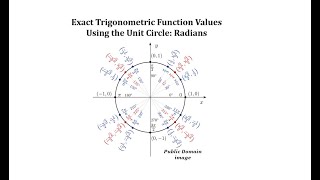
Defining the Unit Circle
Problem 3.39b
Textbook Question
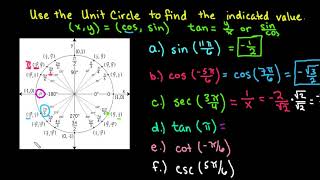
Textbook QuestionFind a calculator approximation to four decimal places for each circular function value. See Example 3. csc (―9.4946)
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
0m:0sPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Cosecant Function
The cosecant function, denoted as csc, is the reciprocal of the sine function. For any angle θ, csc(θ) = 1/sin(θ). This means that to find the cosecant of an angle, one must first determine the sine of that angle and then take its reciprocal. Understanding this relationship is crucial for calculating csc values accurately.
Recommended video:

Graphs of Secant and Cosecant Functions
Calculator Functions
Using a scientific calculator effectively is essential for approximating trigonometric functions. Most calculators have dedicated buttons for sine, cosine, and tangent, as well as their reciprocals. Familiarity with how to input angles in radians or degrees, depending on the calculator's settings, is necessary to obtain correct results for functions like csc.
Recommended video:

How to Use a Calculator for Trig Functions
Radian Measure
Radian measure is a way of measuring angles based on the radius of a circle. One radian is the angle formed when the arc length is equal to the radius. In trigonometry, many functions are often evaluated in radians, so converting degrees to radians or understanding when to use radians is vital for accurate calculations, especially when dealing with non-standard angles.
Recommended video:

Converting between Degrees & Radians

 6:11m
6:11mWatch next
Master Introduction to the Unit Circle with a bite sized video explanation from Callie Rethman
Start learningRelated Videos
Related Practice