Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
7. Non-Right Triangles
Law of Cosines
Problem 7.13
Textbook Question
Solve each triangle. Approximate values to the nearest tenth.
<IMAGE>
 Verified step by step guidance
Verified step by step guidance1
<insert step 1: Identify the given information in the triangle, such as angles and sides. If the image is not available, assume typical triangle information like two angles and one side (AAS or ASA) or two sides and one angle (SAS or SSA).>
<insert step 2: Use the Law of Sines or Law of Cosines to find the unknown sides or angles. For example, if you have two angles and one side, use the Law of Sines: \( \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} \).>
<insert step 3: If using the Law of Sines, solve for the unknown side or angle by cross-multiplying and isolating the variable. If using the Law of Cosines, apply the formula: \( c^2 = a^2 + b^2 - 2ab \cos C \) to find the unknown side.>
<insert step 4: Once you have found one unknown side or angle, use the triangle sum theorem (sum of angles in a triangle is 180 degrees) to find any remaining unknown angles.>
<insert step 5: Double-check your calculations and ensure all angles and sides are consistent with the triangle's properties. Round your answers to the nearest tenth as required.>
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
0m:0sPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Triangle Types
Understanding the types of triangles—such as scalene, isosceles, and equilateral—is essential for solving triangle problems. Each type has unique properties that affect the relationships between its sides and angles, which can influence the methods used for solving them.
Recommended video:
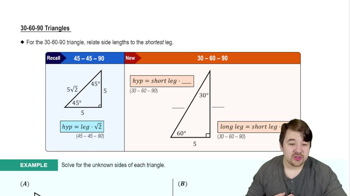
30-60-90 Triangles
Trigonometric Ratios
Trigonometric ratios (sine, cosine, and tangent) relate the angles of a triangle to the lengths of its sides. These ratios are fundamental for solving triangles, especially when using the right triangle definitions or the laws of sines and cosines for non-right triangles.
Recommended video:

Introduction to Trigonometric Functions
Laws of Sines and Cosines
The Law of Sines and the Law of Cosines are critical for solving triangles that are not right-angled. The Law of Sines relates the ratios of sides to the sines of their opposite angles, while the Law of Cosines provides a way to find a side or angle when two sides and the included angle are known.
Recommended video:

Intro to Law of Cosines

 4:35m
4:35mWatch next
Master Intro to Law of Cosines with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice








