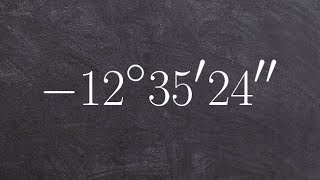Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
1. Measuring Angles
Angles in Standard Position
Problem 7a
Textbook Question
Convert decimal degrees to degrees, minutes, seconds, and convert degrees, minutes, seconds to decimal degrees. If applicable, round to the nearest second or the nearest thousandth of a degree. 119° 08' 03"
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the problem. We need to convert the angle given in degrees, minutes, and seconds (DMS) format, 119° 08' 03", into decimal degrees.
Step 2: Recall the conversion formula. To convert from DMS to decimal degrees, use the formula: \( ext{Decimal Degrees} = ext{Degrees} + \frac{ ext{Minutes}}{60} + \frac{ ext{Seconds}}{3600} \).
Step 3: Substitute the given values into the formula. Here, Degrees = 119, Minutes = 8, and Seconds = 3.
Step 4: Calculate each component: \( \frac{8}{60} \) for minutes and \( \frac{3}{3600} \) for seconds, then add these to the degrees.
Step 5: Sum the values to get the final result in decimal degrees, rounding to the nearest thousandth if necessary.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?

 5:50m
5:50mWatch next
Master Drawing Angles in Standard Position with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice