Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
7. Non-Right Triangles
Law of Sines
Problem 7.48
Textbook Question
Find the area of each triangle using the formula 𝓐 = ½ bh, and then verify that the formula 𝓐 = ½ ab sin C gives the same result.
<IMAGE>
 Verified step by step guidance
Verified step by step guidance1
Identify the base (b) and height (h) of the triangle from the given image.
Use the formula \( \mathcal{A} = \frac{1}{2} b h \) to calculate the area of the triangle.
Identify the sides (a and b) and the included angle (C) from the given image.
Use the formula \( \mathcal{A} = \frac{1}{2} ab \sin C \) to calculate the area of the triangle.
Compare the results from both formulas to verify they give the same area.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
0m:0sPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Area of a Triangle
The area of a triangle can be calculated using the formula A = ½ bh, where 'b' is the base and 'h' is the height. This formula is derived from the fact that a triangle is essentially half of a rectangle formed by the base and height. Understanding this formula is crucial for calculating the area of triangles in various contexts.
Recommended video:
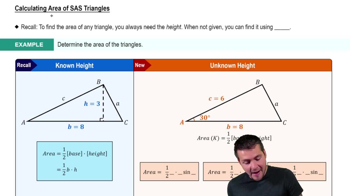
Calculating Area of SAS Triangles
Trigonometric Functions
Trigonometric functions, such as sine, cosine, and tangent, relate the angles of a triangle to the lengths of its sides. The formula A = ½ ab sin C uses the sine of angle C to find the area of a triangle when two sides and the included angle are known. This concept is essential for solving problems involving non-right triangles.
Recommended video:

Introduction to Trigonometric Functions
Verification of Area Formulas
Verifying that different formulas yield the same area involves substituting known values and ensuring consistency between the results. In this case, comparing A = ½ bh with A = ½ ab sin C demonstrates the relationship between the height and the sine of the angle in a triangle. This verification reinforces the understanding of how different geometric properties are interconnected.
Recommended video:

Calculating Area of ASA Triangles

 4:27m
4:27mWatch next
Master Intro to Law of Sines with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice


















