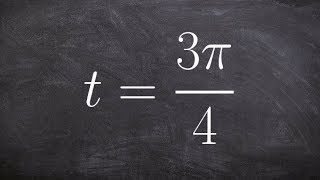Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
3. Unit Circle
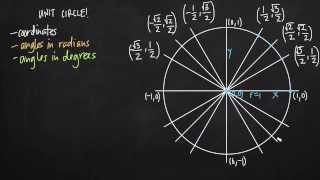
Defining the Unit Circle
Problem 3.19a
Textbook Question
Textbook QuestionUse the formula ω = θ/t to find the value of the missing variable.
θ = 2π/9 radian , ω = 5π/27 radian per min
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
0m:0sPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Angular Displacement (θ)
Angular displacement, represented by θ, measures the angle through which an object has rotated about a fixed point. It is typically expressed in radians, where one complete revolution corresponds to 2π radians. In this question, θ is given as 2π/9 radians, indicating a specific fraction of a full rotation.
Angular Velocity (ω)
Angular velocity, denoted by ω, quantifies the rate of change of angular displacement over time. It is expressed in radians per unit time, such as radians per minute. In the provided question, ω is given as 5π/27 radians per minute, indicating how quickly the object is rotating.
Recommended video:

Introduction to Vectors
Time (t)
Time (t) in the context of angular motion refers to the duration over which the angular displacement occurs. It is a crucial variable in the formula ω = θ/t, as it allows us to relate the angular displacement to the angular velocity. By rearranging the formula, we can solve for the missing time variable when the other two are known.
Recommended video:

Parameterizing Equations

 6:11m
6:11mWatch next
Master Introduction to the Unit Circle with a bite sized video explanation from Callie Rethman
Start learningRelated Videos
Related Practice