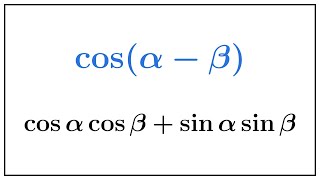Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
6. Trigonometric Identities and More Equations
Sum and Difference Identities
Problem 5.44b
Textbook Question
Textbook QuestionWrite each function as an expression involving functions of θ or x alone. See Example 2.
tan(180° + θ)
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
0m:0sPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Trigonometric Functions
Trigonometric functions, such as sine, cosine, and tangent, relate the angles of a triangle to the lengths of its sides. They are periodic functions that have specific values for standard angles, which can be used to simplify expressions involving angles. Understanding these functions is essential for manipulating and transforming trigonometric expressions.
Recommended video:

Introduction to Trigonometric Functions
Angle Addition Formulas
Angle addition formulas provide a way to express trigonometric functions of sums or differences of angles in terms of the functions of the individual angles. For example, the tangent addition formula states that tan(A + B) = (tan A + tan B) / (1 - tan A tan B). These formulas are crucial for rewriting expressions like tan(180° + θ) in terms of θ alone.
Recommended video:

Quadratic Formula
Periodic Properties of Trigonometric Functions
Trigonometric functions exhibit periodic behavior, meaning they repeat their values in regular intervals. For instance, the tangent function has a period of 180°, which implies that tan(θ + 180°) = tan(θ). Recognizing these properties allows for simplification of expressions involving angles that exceed standard ranges, such as transforming tan(180° + θ) into a more manageable form.
Recommended video:

Period of Sine and Cosine Functions

 6:14m
6:14mWatch next
Master Sum and Difference of Sine & Cosine with a bite sized video explanation from Callie Rethman
Start learningRelated Videos
Related Practice