Concept Check Suppose that the point (x, y) is in the indicated quadrant. Determine whether the given ratio is positive or negative. Recall that r = √(x² + y²) .(Hint: Drawing a sketch may help.) IV , x/y

Verified step by step guidance

1. <insert step 1> Draw a coordinate plane and label the quadrants. Quadrant IV is located in the lower right section of the plane.>
2. <insert step 2> Recall the signs of x and y in Quadrant IV: x is positive and y is negative.>
3. <insert step 3> Consider the ratio x/y. Since x is positive and y is negative, the ratio x/y will be negative.>
4. <insert step 4> Visualize or sketch the point (x, y) in Quadrant IV to reinforce the understanding of the signs of x and y.>
5. <insert step 5> Conclude that in Quadrant IV, the ratio x/y is negative.>

Key Concepts

Quadrants of the Cartesian Plane

The Cartesian plane is divided into four quadrants based on the signs of the x and y coordinates. In Quadrant IV, x is positive and y is negative. Understanding the signs of coordinates in each quadrant is essential for determining the positivity or negativity of trigonometric ratios.

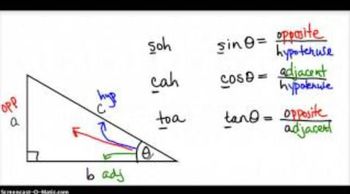
Trigonometric Ratios

Trigonometric ratios, such as sine, cosine, and tangent, are defined based on the relationships between the sides of a right triangle. For the ratio x/y, this represents the tangent function. Knowing how these ratios behave in different quadrants helps in assessing their signs.

Distance Formula and Radius (r)

The radius r is calculated using the formula r = √(x² + y²), which represents the distance from the origin to the point (x, y). In Quadrant IV, since x is positive and y is negative, r will always be positive. This concept is crucial for understanding the geometric interpretation of trigonometric functions.