Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
6. Trigonometric Identities and More Equations
Introduction to Trigonometric Identities
Problem 5.41a
Textbook Question
For each expression in Column I, choose the expression from Column II that completes an identity. One or both expressions may need to be rewritten.
sec x/csc x
 Verified step by step guidance
Verified step by step guidance1
Step 1: Recall the definitions of secant and cosecant. \( \sec x = \frac{1}{\cos x} \) and \( \csc x = \frac{1}{\sin x} \).
Step 2: Rewrite the given expression \( \frac{\sec x}{\csc x} \) using the definitions: \( \frac{\frac{1}{\cos x}}{\frac{1}{\sin x}} \).
Step 3: Simplify the expression by multiplying the numerator and the denominator by \( \sin x \cdot \cos x \) to eliminate the fractions.
Step 4: After simplification, the expression becomes \( \frac{\sin x}{\cos x} \).
Step 5: Recognize that \( \frac{\sin x}{\cos x} \) is the definition of \( \tan x \). Thus, the expression simplifies to \( \tan x \).
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
0m:0sPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Trigonometric Identities
Trigonometric identities are equations that involve trigonometric functions and are true for all values of the variables involved. Common identities include the Pythagorean identities, reciprocal identities, and co-function identities. Understanding these identities is crucial for simplifying expressions and solving equations in trigonometry.
Recommended video:

Fundamental Trigonometric Identities
Reciprocal Functions
Reciprocal functions in trigonometry refer to pairs of functions where one function is the reciprocal of another. For example, the secant function (sec x) is the reciprocal of the cosine function (cos x), and the cosecant function (csc x) is the reciprocal of the sine function (sin x). Recognizing these relationships helps in rewriting expressions and solving trigonometric identities.
Recommended video:
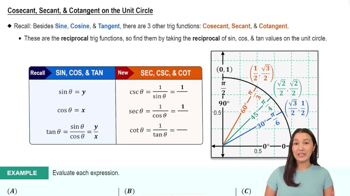
Secant, Cosecant, & Cotangent on the Unit Circle
Simplifying Trigonometric Expressions
Simplifying trigonometric expressions involves rewriting them in a more manageable form, often using identities. This process may include factoring, combining fractions, or substituting equivalent functions. Mastery of simplification techniques is essential for effectively completing identities and solving trigonometric problems.
Recommended video:

Simplifying Trig Expressions

 6:19m
6:19mWatch next
Master Even and Odd Identities with a bite sized video explanation from Callie Rethman
Start learningRelated Videos
Related Practice