Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
5. Inverse Trigonometric Functions and Basic Trigonometric Equations
Linear Trigonometric Equations
Problem 41
Textbook Question
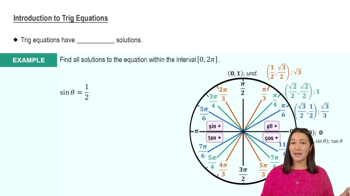
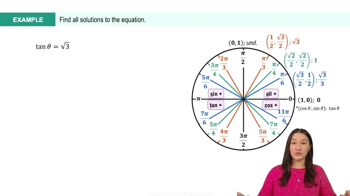
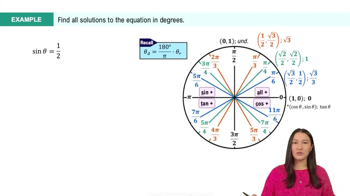
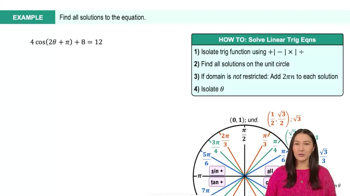
Textbook QuestionExercises 39–52 involve trigonometric equations quadratic in form. Solve each equation on the interval [0, 2𝝅). 2 cos² x + 3 cos x + 1 = 0
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
11mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Quadratic Equations
A quadratic equation is a polynomial equation of the form ax² + bx + c = 0, where a, b, and c are constants, and a ≠ 0. In trigonometry, we often encounter quadratic equations in terms of trigonometric functions, such as cos² x or sin² x. These equations can be solved using factoring, completing the square, or the quadratic formula.
Recommended video:

Introduction to Quadratic Equations
Trigonometric Identities
Trigonometric identities are equations that involve trigonometric functions and are true for all values of the variable where both sides are defined. Common identities include the Pythagorean identities, angle sum and difference identities, and double angle formulas. Understanding these identities is crucial for simplifying trigonometric equations and solving them effectively.
Recommended video:

Fundamental Trigonometric Identities
Interval Notation
Interval notation is a mathematical notation used to represent a range of values. In this context, the interval [0, 2π) indicates that the solutions to the trigonometric equation should be found within the range starting from 0 (inclusive) to 2π (exclusive). This is important for determining valid solutions in trigonometric problems, as trigonometric functions are periodic.
Recommended video:

i & j Notation

 4:25m
4:25mWatch next
Master Introduction to Trig Equations with a bite sized video explanation from Callie Rethman
Start learning