Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
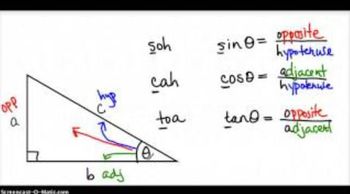
2. Trigonometric Functions on Right Triangles
Trigonometric Functions on Right Triangles
Problem 14a
Textbook Question
Textbook QuestionConcept Check The two methods of expressing bearing can be interpreted using a rectangular coordinate system. Suppose that an observer for a radar station is located at the origin of a coordinate system. Find the bearing of an airplane located at each point. Express the bearing using both methods. (0, -2)
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Bearing
Bearing is a method of expressing direction relative to a reference point, typically measured in degrees from the north. It indicates the direction one must travel to reach a specific point, with angles measured clockwise from true north. For example, a bearing of 90° indicates an eastward direction, while a bearing of 180° points directly south.
Rectangular Coordinate System
A rectangular coordinate system, also known as the Cartesian coordinate system, uses two perpendicular axes (x and y) to define the position of points in a plane. The origin (0,0) is the intersection of these axes, and points are represented as ordered pairs (x, y). This system is essential for visualizing and calculating distances and angles in trigonometry.
Recommended video:

Intro to Polar Coordinates
Conversion of Coordinates to Bearings
To convert coordinates to bearings, one must determine the angle formed by the line connecting the origin to the point and the north direction. This involves calculating the arctangent of the ratio of the y-coordinate to the x-coordinate, adjusting the angle based on the quadrant in which the point lies. For the point (0, -2), the bearing would be directly south, or 180°.
Recommended video:

Intro to Polar Coordinates

 6:4m
6:4mWatch next
Master Introduction to Trigonometric Functions with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice