Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
10. Parametric Equations
Graphing Parametric Equations
Problem 8.32
Textbook Question
Textbook QuestionGraph each plane curve defined by the parametric equations for t in [0, 2π] Then find a rectangular equation for the plane curve. See Example 3.
x = 4 sin t , y = 3 cos t
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
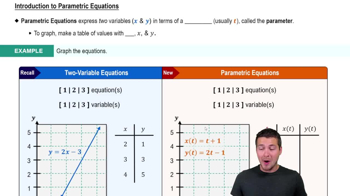
Parametric Equations
Parametric equations express the coordinates of points on a curve as functions of a variable, typically denoted as 't'. In this case, x and y are defined in terms of the parameter t, allowing for the representation of curves that may not be easily described by a single equation. Understanding how to manipulate and graph these equations is essential for visualizing the curve they represent.
Recommended video:

Parameterizing Equations
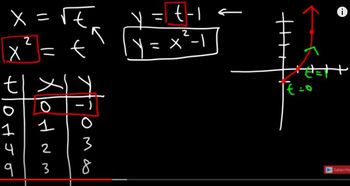
Graphing Techniques
Graphing techniques involve plotting points on a coordinate system based on the values derived from the parametric equations. For the given equations, x = 4 sin t and y = 3 cos t, one would calculate the values of x and y for various t values within the specified range [0, 2π]. This process helps in visualizing the shape and behavior of the curve, which in this case represents an ellipse.
Recommended video:
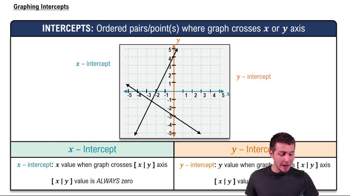
Graphing Intercepts
Rectangular Equation
A rectangular equation eliminates the parameter t to express the relationship between x and y directly. By using trigonometric identities, such as sin²(t) + cos²(t) = 1, one can derive a single equation that describes the curve in Cartesian coordinates. For the given parametric equations, this results in the equation of an ellipse, which can be derived by substituting the expressions for x and y.
Recommended video:

Convert Equations from Rectangular to Polar

 4:47m
4:47mWatch next
Master Introduction to Parametric Equations with a bite sized video explanation from Patrick Ford
Start learning