Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
0. Review of College Algebra
Basics of Graphing
Problem 55
Textbook Question
In the following exercises, (a) find the center-radius form of the equation of each circle described, and (b) graph it. See Examples 5 and 6. center (0, 4), radius 4
 Verified step by step guidance
Verified step by step guidance1
<insert step 1: Start by recalling the standard form of the equation of a circle, which is (x - h)^2 + (y - k)^2 = r^2, where (h, k) is the center of the circle and r is the radius.>
<insert step 2: Identify the center (h, k) and the radius r from the problem. Here, the center is (0, 4) and the radius is 4.>
<insert step 3: Substitute the center (0, 4) and the radius 4 into the standard form equation. This gives you (x - 0)^2 + (y - 4)^2 = 4^2.>
<insert step 4: Simplify the equation. Since (x - 0)^2 is just x^2, the equation becomes x^2 + (y - 4)^2 = 16.>
<insert step 5: To graph the circle, plot the center at (0, 4) on the coordinate plane, and draw a circle with a radius of 4 units around this center.>
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
0m:0sPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Center-Radius Form of a Circle
The center-radius form of a circle's equation is expressed as (x - h)² + (y - k)² = r², where (h, k) is the center of the circle and r is the radius. This format allows for easy identification of the circle's center and radius, facilitating both graphing and analysis.
Recommended video:

Introduction to the Unit Circle
Graphing a Circle
To graph a circle, one starts by plotting its center on the coordinate plane. From the center, the radius is used to mark points in all directions (up, down, left, right) to outline the circle. Connecting these points smoothly creates the circular shape, ensuring that all points are equidistant from the center.
Recommended video:

Introduction to the Unit Circle
Distance Formula
The distance formula, derived from the Pythagorean theorem, calculates the distance between two points in a plane. It is given by d = √((x₂ - x₁)² + (y₂ - y₁)²). This concept is essential for verifying that points on the graph maintain a constant distance (the radius) from the center of the circle.
Recommended video:

Quadratic Formula

 5:1m
5:1mWatch next
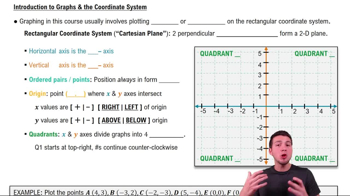
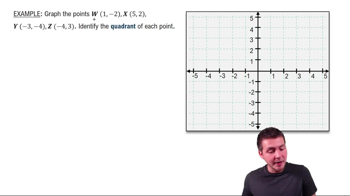
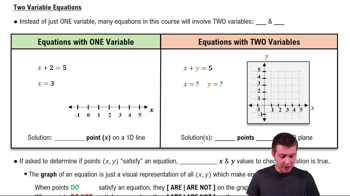
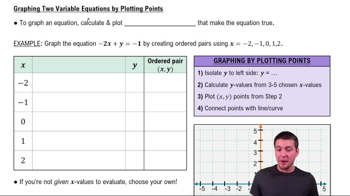
Master Introduction to Graphs & the Coordinate System with a bite sized video explanation from Patrick Ford
Start learning