Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
8. Vectors
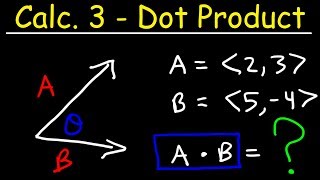
Dot Product
Problem 23
Textbook Question
Textbook QuestionIn Exercises 23–32, use the dot product to determine whether v and w are orthogonal. v = i + j, w = i - j
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Dot Product
The dot product is a mathematical operation that takes two vectors and returns a scalar. It is calculated by multiplying corresponding components of the vectors and summing the results. For vectors v = (v1, v2) and w = (w1, w2), the dot product is given by v · w = v1*w1 + v2*w2. This operation is crucial for determining the angle between vectors and checking for orthogonality.
Recommended video:

Introduction to Dot Product
Orthogonal Vectors
Two vectors are considered orthogonal if they are perpendicular to each other, which occurs when their dot product equals zero. This property is significant in various applications, including physics and computer graphics, as it indicates that the vectors do not influence each other in their respective directions. Understanding orthogonality helps in simplifying problems involving vector components.
Recommended video:

Introduction to Vectors
Vector Representation
Vectors can be represented in terms of their components along the coordinate axes. In this case, the vectors v = i + j and w = i - j can be expressed as v = (1, 1) and w = (1, -1). This representation allows for straightforward calculations, such as the dot product, and aids in visualizing the vectors in a Cartesian plane, facilitating the analysis of their relationships.
Recommended video:

Introduction to Vectors

 5:40m
5:40mWatch next
Master Introduction to Dot Product with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice