Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
2. Trigonometric Functions on Right Triangles
Trigonometric Functions on Right Triangles
Problem 28b
Textbook Question
Textbook QuestionDetermine the signs of the trigonometric functions of an angle in standard position with the given measure. See Example 2. 84°
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Standard Position of an Angle
An angle is in standard position when its vertex is at the origin of a coordinate system and its initial side lies along the positive x-axis. The angle is measured counterclockwise from the initial side. Understanding this concept is crucial for determining the location of the terminal side of the angle and subsequently the signs of the trigonometric functions.
Recommended video:

Drawing Angles in Standard Position
Quadrants of the Coordinate Plane
The coordinate plane is divided into four quadrants, each defined by the signs of the x and y coordinates. In Quadrant I, both x and y are positive; in Quadrant II, x is negative and y is positive; in Quadrant III, both are negative; and in Quadrant IV, x is positive and y is negative. The quadrant in which the terminal side of the angle lies determines the signs of the sine, cosine, and tangent functions.
Recommended video:

Quadratic Formula
Signs of Trigonometric Functions
The signs of the six trigonometric functions (sine, cosine, tangent, cosecant, secant, and cotangent) depend on the quadrant in which the angle's terminal side is located. In Quadrant I, all functions are positive; in Quadrant II, sine and cosecant are positive; in Quadrant III, tangent and cotangent are positive; and in Quadrant IV, cosine and secant are positive. This knowledge is essential for accurately determining the values of these functions for any given angle.
Recommended video:

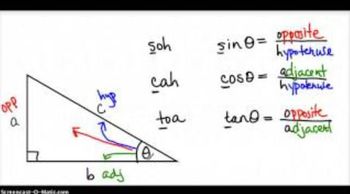
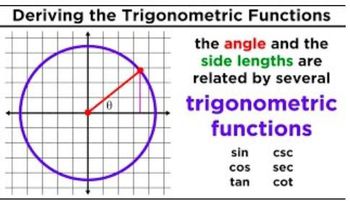
Introduction to Trigonometric Functions

 6:4m
6:4mWatch next
Master Introduction to Trigonometric Functions with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice