Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
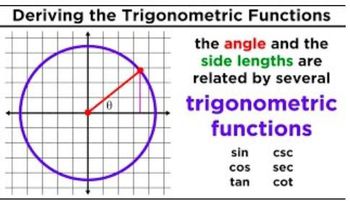
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
2. Trigonometric Functions on Right Triangles
Trigonometric Functions on Right Triangles
Problem 72
Textbook Question
Textbook QuestionIf θ is an acute angle and cos θ = 1/3, find csc (𝜋/2 - θ).
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Trigonometric Functions
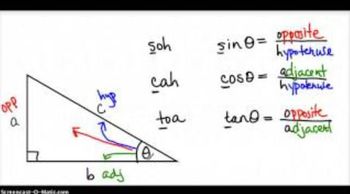
Trigonometric functions relate the angles of a triangle to the lengths of its sides. The primary functions include sine, cosine, and tangent, which are defined for acute angles in a right triangle. Understanding these functions is essential for solving problems involving angles and their relationships.
Recommended video:

Introduction to Trigonometric Functions
Cofunction Identity
Cofunction identities express the relationship between the sine and cosine of complementary angles. Specifically, csc(π/2 - θ) is equal to sin(θ). This identity is crucial for transforming expressions involving trigonometric functions and simplifying calculations.
Recommended video:

Cofunction Identities
Reciprocal Functions
Reciprocal functions in trigonometry include cosecant (csc), secant (sec), and cotangent (cot), which are the reciprocals of sine, cosine, and tangent, respectively. For example, csc(θ) = 1/sin(θ). Recognizing these relationships helps in finding values of trigonometric functions based on known values.
Recommended video:
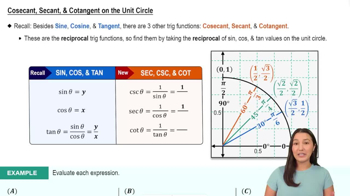
Secant, Cosecant, & Cotangent on the Unit Circle

 6:4m
6:4mWatch next
Master Introduction to Trigonometric Functions with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice