Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
3. Unit Circle
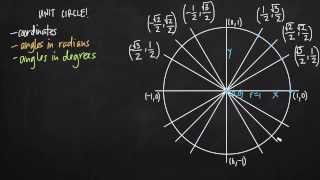
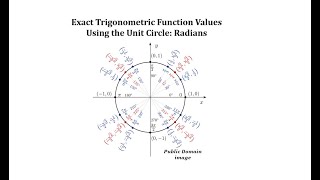
Defining the Unit Circle
Problem 3.27b
Textbook Question
Find each exact function value. See Example 2.
sin (4π/3)
 Verified step by step guidance
Verified step by step guidance1
Identify the reference angle for \(\frac{4\pi}{3}\). The reference angle is the angle in the first quadrant that corresponds to \(\frac{4\pi}{3}\). Since \(\frac{4\pi}{3}\) is in the third quadrant, subtract \(\pi\) to find the reference angle: \(\frac{4\pi}{3} - \pi = \frac{\pi}{3}\).
Determine the sine of the reference angle. The sine of \(\frac{\pi}{3}\) is known from the unit circle to be \(\frac{\sqrt{3}}{2}\).
Consider the sign of the sine function in the third quadrant. In the third quadrant, both sine and cosine are negative.
Apply the sign to the sine value of the reference angle. Since sine is negative in the third quadrant, \(\sin(\frac{4\pi}{3}) = -\sin(\frac{\pi}{3})\).
Combine the results to find the exact value: \(\sin(\frac{4\pi}{3}) = -\frac{\sqrt{3}}{2}\).
Was this helpful?

 6:11m
6:11mWatch next
Master Introduction to the Unit Circle with a bite sized video explanation from Callie Rethman
Start learningRelated Videos
Related Practice