Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
0. Review of College Algebra
Basics of Graphing
Problem 39
Textbook Question
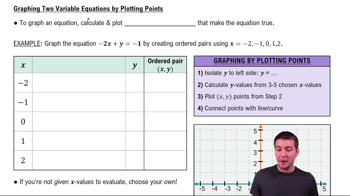
Textbook QuestionFor each equation, (a) give a table with at least three ordered pairs that are solutions, and (b) graph the equation. See Examples 3 and 4. y = x³
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
7mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Ordered Pairs
Ordered pairs are pairs of numbers that represent coordinates on a Cartesian plane, typically written as (x, y). In the context of the equation y = x³, each x-value corresponds to a specific y-value calculated by cubing x. For example, if x = 1, then y = 1³ = 1, giving the ordered pair (1, 1). Generating multiple ordered pairs helps visualize the relationship defined by the equation.
Recommended video:

Determining Different Coordinates for the Same Point
Graphing Functions
Graphing functions involves plotting the ordered pairs on a coordinate plane to visualize the relationship between the variables. For the equation y = x³, the graph will show how y changes as x varies, creating a curve that passes through the origin and extends into the first and third quadrants. Understanding how to graph functions is essential for interpreting their behavior and identifying key features such as intercepts and symmetry.
Recommended video:

Graph of Sine and Cosine Function
Cubic Functions
Cubic functions are polynomial functions of degree three, characterized by the general form y = ax³ + bx² + cx + d, where a, b, c, and d are constants. The specific function y = x³ is a simple cubic function where a = 1, and it exhibits unique properties such as having one inflection point and no local maxima or minima. Recognizing the characteristics of cubic functions is crucial for understanding their graphs and behavior.
Recommended video:
Graphs of Common Functions

 5:1m
5:1mWatch next
Master Introduction to Graphs & the Coordinate System with a bite sized video explanation from Patrick Ford
Start learning